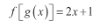Classificação das funções
Função Composta
Função Composta - Análise Gráfica
Função Inversa
Função inversa
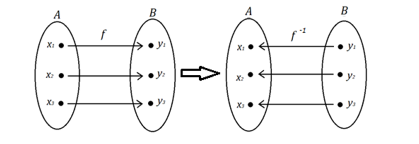
Definimos função inversa (f -1) de uma função f do seguinte modo:
Ou seja, para todo par ordenado (a, b) pertencente à função f, existe um par ordenado (b, a) correspondente na função inversa f -1.

Condição de existência
A relação inversa de f: A → B é uma função f -1: B → A, se e somente se, f é uma função bijetora.
Lei de formação
Para encontrarmos a lei de formação de uma função inversa, devemos seguir os seguintes passos:
- Na lei de formação de f, devemos trocar o y por x e o x por y.
- Depois, devemos isolar o novo y.
Ex: Vamos achar a inversa de f(x) = x + 1.
- y = x + 1
- x = y + 1 (trocando x por y e y por x)
- y = x – 1 = f -1(x)
Gráfico
O gráfico de uma f-1 é simétrico ao gráfico de f em relação à reta y = x, chamada de função identidade.
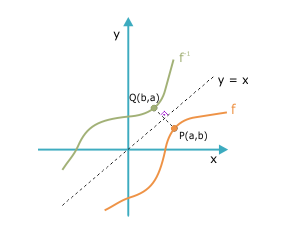
Função composta
Função composta é aquela que tem como abscissa a imagem de outra função.
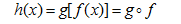
Ou seja, a abscissa de g(x) é a imagem de f(x).
Observe como isso funciona:
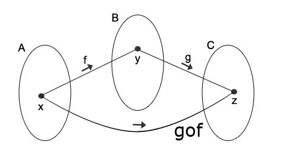
Condição de existência
Para que haja a função composta da função g com a função f, o domínio de g deve ser igual ao contradomínio de f.
Repare que no esquema anterior, f tem como domínio o conjunto A e contradomínio o conjunto B. Já a função g tem como domínio o conjunto B e contradomínio o conjunto C. Ou seja, o domínio de g é igual ao contradomínio de f.
Determinação da função composta
Partimos do exemplo de duas funções f(x) = x + 1 e g(x) = 2x
Calcular f[g(x)] significa encontrar a lei de formação da função composta de g com f. Tendo como base as funções do exemplo, usamos o passo a passo abaixo:
- Partimos de f(x) = x + 1
- Em seguida, substituímos x por g(x): f[g (x)] = g(x) + 1
- Enfim, como g(x) = 2x, temos: g[f(x)] = 2x + 1.
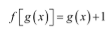
Enfim, como g(x) = 2x, temos: