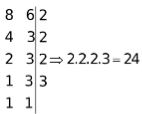Múltiplos e Divisores em Matemática

Multiplos e Divisores

Para falarmos de múltiplos e divisores precisamos definir nosso ambiente de trabalho. 

Neste momento nós trabalharemos dentro do conjunto dos números naturais, ou seja, todas as definições e propriedades que abordaremos funciona para os números N = {0,1,2,3,4,5...}

Considerando dois números naturais, vamos chamá-los de A e B, dizemos que A divide B se existir um terceiro número natural K, tal que B = A * K 

Assim podemos usar algumas nomenclaturas que são equivalentes: 

1. A divide B
2. A é um divisor de B
3. B é divisível por A
4. B é múltiplo de A 

Observando os itens c e d perceba que ser “divisível por” é o mesmo que ser “múltiplo de”. 

 Podemos entender o conceito de divisibilidade através da operação divisão. Se o número natural B, divido pelo natural A for uma divisão exata (resto zero) podemos fazer as mesmas quatro afirmações acima.

Existe uma forma de determinar se um número é divisível por outro sem que de fato tenhamos que efetuar divisão, para isso usamos os critérios de divisibilidade. Cada número tem seu critério de divisibilidade, alguns critérios são mais simples e eficientes que outros.

Números primos 

Definição: Todo número natural maior que 1 que possui somente dois divisores, o 1 e ele mesmo é chamado de número primo. Se um número possui algum divisor além de 1 e dele mesmo, é chamado de número composto, ou seja, este número pode ser escrito como a multiplicação de outros números diferentes de 1 e dele mesmo.

Não existe fórmula para obter os números primos mas é possível demostrar que eles são infinitos. 

Identificando um número primo

Para identificar se um número é primo, basta testar os critérios de divisibilidade dos números primos menores que sua raiz quadrada. Se o número em questão não for divisível por nenhum dos números testados, ele é primo.

Teorema fundamental da Aritmética 

Todo número natural maior ou igual a 2 sempre pode ser decomposto em fatores primos e esta fatoração é única. 

Fatoração em números primos 

Decompor um número em fatores primos é reescreve-lo como uma multiplicação de números primos, para descobrir quais números primos poderemos usar temos que saber quais são os números primos e seus critérios de divisibilidade.

MMC e MDC

MMC (Mínimo Múltiplo Comum) e MDC (Máximo Divisor Comum) são conceitos fundamentais para a matemática. Para entendê-los, precisamos conhecer os conceitos de divisores e múltiplos. Divisores são quocientes da divisão exata entre dois números.

Exemplo: 5 é divisor de 10 porque 10 dividido por 5 é uma divisão exata (o resto é igual a 0).
O número de divisores de um número é limitado, sendo sempre o menor número o 1 e o maior ele mesmo.

Exemplo: Para sabermos o MDC entre 10 e 20 precisamos conhecer os divisores de 10 e 20.

Os de 10 são: 1,2,5 e 10 e de 20 são: 1,2,4,5,10,20. Logo o conjunto de divisores comuns é {1,2,10}, assim o MDC é 10, ou seja, é o maior número que divide os dois números ao mesmo tempo.

Observação: Caso os números não possuam MDC = 1 eles são primos entre si.

Um processo prático é fatorar os dois números simultaneamente em fatores primos e ver quais números dividem eles ao mesmo tempo. O produto entre eles será o MDC.

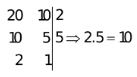
Já o conceito de múltiplo de um número natural se refere ao produto desse número por outro número natural, incluindo o zero. Vale lembrar que o zero é múltiplo de todos os números (o produto de qualquer número por 0 é igual a 0). Por exemplo: os múltiplos de 5 são: 0,5,10,15… Note que o 5 é divisor de 10 e o 10 é múltiplo de 5 e que o conjunto dos múltiplos é infinito. Para descobrirmos o mínimo múltiplo comum entre dois ou mais números, basta conhecer o primeiro número que sejam múltiplos dos números ao mesmo tempo.

 
Exemplo: Para descobrirmos o MMC entre 6 e 8 analisaremos seus múltiplos. Os de 6 são: 0,6,12,18,24,… e os de 8 são 0,8,16,24,… Assim o conjunto dos múltiplos em comum é {0,24,…} assim o MMC é 24.
O processo prático é parecido com o do MDC, porém fatoraremos os números em fatores primos até chegarmos a 1. O produto entre eles será o MMC.