Descubra o que é função quadrática com um resumo que vai te desvendar todos os conceitos sobre o tema! Prepare-se para o ENEM e vestibulares!
Função quadrática ou função do segundo grau é uma aplicação F de →
que associa a cada x o elemento (ax² + bx + c) ∈
, em que a, b e c são números reais dados e a ≠ 0. Pois se a = 0, não teremos mais uma função quadrática e sim uma função afim: y = bx +c.
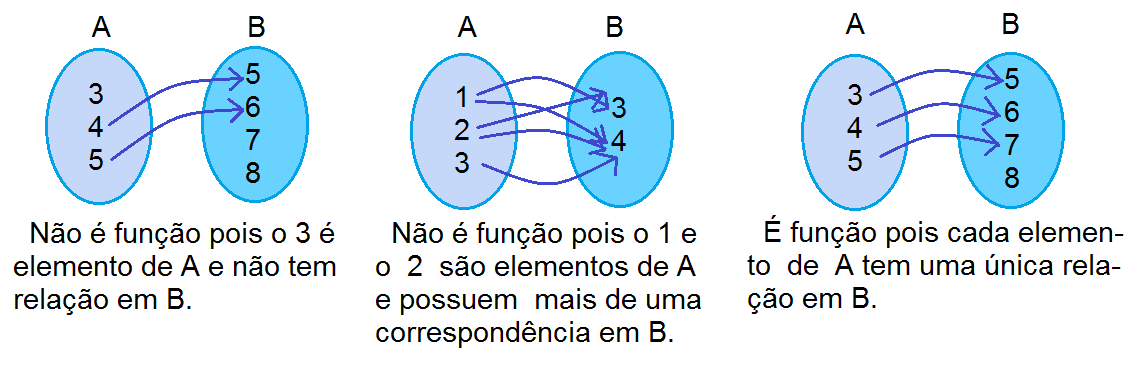
Relembrando: O que é função?
Sendo A e B conjuntos não vazios, uma relação F de A → B (lê-se A em B) é denominada aplicação de A – domínio, conjunto de partida – em B – contradomínio, conjunto de chegada –, ou função definida em A com imagens em B se para todo x ∈ A existe um só y ∈ B, tal que (x,y) ∈ F.
Exemplos de funções quadráticas:
- 2x² + 5x + 7, em que a = 2, b = 5 e c = 7.
- -x², em que a = -1 e b = c = 0.
- x² + x + 1, em que a = b = c = 1.
- 6x² + 5, em que a = 6, b = 0 e c = 5.
Gráfico da Função Quadrática
O gráfico da função quadrática é uma parábola (isso será provado em Geometria Analítica):
Concavidade
A parábola representativa da função quadrática pode ter sua concavidade voltada para cima ou para baixo. Isso dependerá do sinal de a:
- Se a > 0, a concavidade será voltada para cima.
- Se a < 0, a concavidade será voltada para baixo.

Forma Canônica
A construção do gráfico da função quadrática através de uma tabela de valores de x e de y nem sempre é precisa, pois pode acontecer que em certa função o valor da abscissa (valor de x) ou da ordenada (valor de y) não seja inteiro.
Para iniciarmos um estudo mais detalhado da função, vamos transformá-la em outra forma mais adequada, chamada forma canônica.
Portanto, a forma canônica da função quadrática é:Zeros da Função Quadrática
Os zeros ou raízes da função são os valores de x para os quaisObservemos que, para existir raízes reais na equação do segundo grau, precisamos que seja real. Logo, temos três casos:
i) e, portanto, a equação apresentará duas raízes reais e distintas, que serão:
.
ii) e, portanto, a equação apresentará duas raízes reais e iguais, que serão:
.
iii) e sabemos que, neste caso,
, portanto, diremos que a equação não apresentará raízes reais.
Interpretando geometricamente, os zeros da função quadrática são as abscissas dos pontos onde a parábola corta o eixo x.
Máximo e Mínimo
Sendo o conjunto imagem, dizemos que
é o valor de máximo da função
se, e somente se,
para qualquer
. E então, o número
, sendo
o conjunto domínio, é chamado de ponto de máximo da função.
Dizemos que é o valor de mínimo da função
se, e somente se,
para qualquer
. E então, o número
é chamado de ponto de mínimo da função.
Sucintamente, podemos dizer que:
i) Se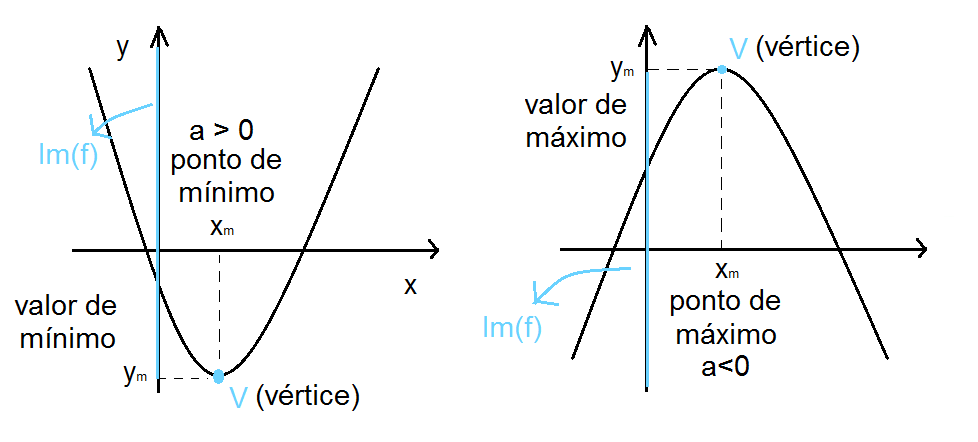
Vértice da Parábola
O pontoFontes de Pesquisa
Fundamentos da Matemática Elementar - Volume 1; Iezzi, Gelson; Murakami, Carlos. Oitava Edição - São Paulo: Atual, 2004.
Exercícios
1. (ENEM – 2009) Um posto de combustível vende 10.000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10.200 litros. Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é:a) V = 10.000 + 50x – x²b) V = 10.000 + 50x + x²c) V = 15.000 – 50x – x²d) V = 15.000 + 50x – x²e) V = 15.000 – 50x + x²
2. (UEL) A função real f, de variável real, dada por f(x)=-x²+12x+20, tem um valor:
a) mínimo igual a -16, para x = 6.b) mínimo igual a 16, para x = -12.c) máximo igual a 56, para x = 6.d) máximo igual a 72, para x = 12.e) máximo igual a 240, para x = 20.
3. (UFMG) Observe a figura.
Nessa figura, está representada a parábola de vértice V, gráfico da função de segundo grau cuja expressão é:a) y = (x² /5) - 2xb) y = x² - 10xc) y = x² + 10xd) y = (x²/5) - 10xe) y = (x²/5) + 10x
GABARITO
1. D
2. C
3. A


