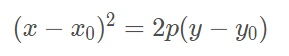Exercícios sobre circunferências e cônicas em Matemática

Circunferência

Definição

Circunferência é o nome dado ao conjunto de pontos do plano equidistantes de um ponto fixo, que chamamos de centro.

Equação da circunferência

Uma circunferência γ de centro no ponto C(x​₀​​,y​₀​​) e raio de medida R é o conjunto dos pontos P(x,y), tais que P ∈ γ, PC​​​ = R.

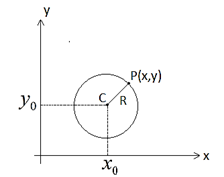
Substituindo PC por seu valor, de acordo com a fórmula da distância entre dois pontos tem-se:

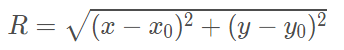
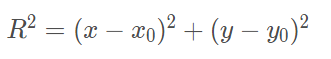
Obs.: Repare que, se o centro da circunferência for em (0, 0), teremos a equação R² = x² + y²

Cônicas

Elipse

Elipse é o conjunto de todos os pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante.

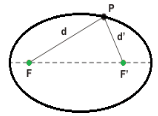
d + d’ = constante = 2a

Elementos de uma elipse

Pela figura, vemos que ​a²​ ​= b​² ​​+ c​²​​. Esta igualdade mostra que b < a e c <  a.

• Focos: são os pontos F_​1​​ e F​₂​​.
• Distância focal: é a distância 2c entre os focos.
• Centro: é o ponto médio C do segmento F​1​​F​2​​.
• Eixo maior: é o segmento A​₁​​A​₂​​ de comprimento 2a.
• Eixo menor: é o segmento B​₁​​B​₂​​ de comprimento 2b e perpendicular a A​₁​​A​₂​​ no seu ponto médio.
• Excentricidade: é o número real e =​​ c/a​​ (0< e <1)

Obs…: A excentricidade é responsável pela “forma” da elipse: elipses com excentricidade perto de 0 são aproximadamente circulares, enquanto que elipses com excentricidade próxima de 1 são “achatadas”.​​ .

Equação Reduzida

Eixo maior é paralelo ao eixo x:

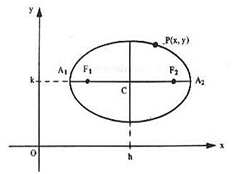
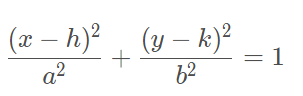
Eixo maior é paralelo ao eixo y:

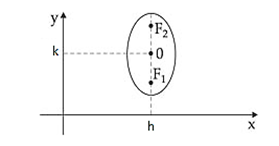
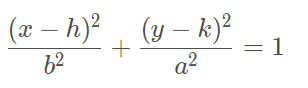
Hipérbole

Hipérbole é o lugar geométrico dos pontos P(x, y) de um plano tal que a diferença (em módulo) de suas distâncias a dois pontos fixos F​₁​​ e F​_2​​ é constante (2a < 2c), com F​₁​​F​₂​​ = 2c.

Eixo de simetria coincide com o eixo x

Considerando o centro O (x​₀​​, y_​0​​)

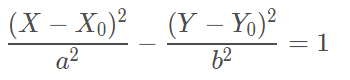
Eixo de simetria coincide com o eixo y

Considerando o centro O (x​_0,y₀)

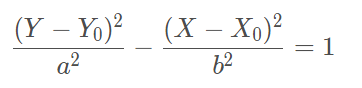
Parábola

Parábola é o lugar geométrico dos pontos do plano que distam igualmente de uma reta fixa d, chamada diretriz, e de um ponto fixo F, não pertencente à diretriz, chamado foco.

Elementos de uma parábola

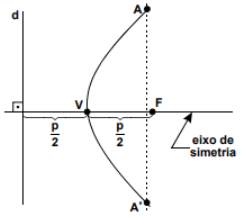
Denominamos:

F: foco
d: diretriz
V: vértice
p: parâmetro, que reprsenta a distância do foco à diretriz
reta VF: eixo de simetria da parábola.

Equação da parábola na forma explícita