Exercício de multiplicação de matrizes 4x4 e 4x1
Exercício de multiplicação de matrizes 3x4 e 4x1
Exercício de matriz simétrica
Exercício sobre a relação de sistemas lineares com matrizes
Exercício sobre coordenadas dos elementos de uma matriz
Exercício sobre multiplicação com matriz identidade
Exercício sobre equação de matrizes
Matrizes
Multiplicação de matrizes
→ Multiplicação de um número real por uma matriz:
Considere um número real k. Multiplicar este número real por uma matriz qualquer é simplesmente multiplicar todos os elementos dessa matriz por esse número k.
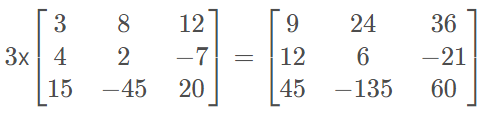
→ Multiplicação entre matrizes:
Condição para existência do produto:
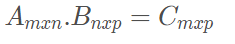
Assim, o número de colunas de A deve ser igual ao de linhas de B. Se isso acontecer , o resultado será uma matriz C com o número de linhas de A e colunas de B.
Multiplicação: linhas da primeira matriz são multiplicados por colunas da segunda matriz.
Exemplo 1:
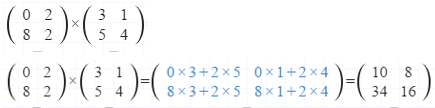
Exemplo 2:
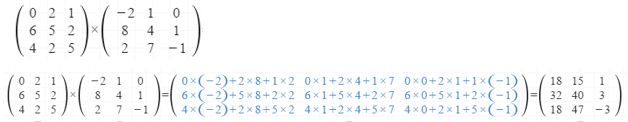
Matriz Inversa
Dada a matriz quadrada A, dizemos que A é invertível (ou não singular), se e somente se existir uma matriz X, tal que A.X = I, onde I é a matriz identidade. Uma notação comum para a matriz inversa é A elevado a -1.
Exemplo:
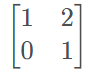
Descobrir a matriz inversa é o mesmo que descobrir valores de x,y,z,w em
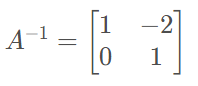
Efetuando o produto das matrizes:
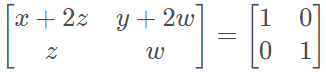
Usando a igualdade das matrizes:
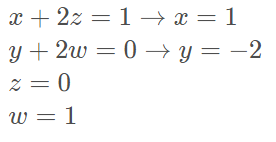
Substituindo, descobrimos que
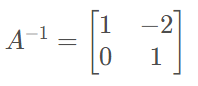
Não é sempre que a matriz possui inversa, pois o sistema pode não ter solução. Em aulas posteriores, aprenderemos um método prático para a existência ou não de inversa.