Exercícios envolvendo logaritmos em Matemática

Logaritmos

Definimos como logaritmo de um número positivo a na base b o valor do expoente da potência de base b que tem como resultado o número a.

Ou seja:

log_ba ↔ b​^x ​​= a

Chamamos a de logaritmando e b de base

Ex: log₂8 = 3 pois 2³ = 8

Condição de existência

Para que log_ba esteja definido duas condições devem ser atendidas:

1) Base: b > 0 e b ≠ 1

2) Logaritmando: a > 0

Essas condições são fundamentais na resolução de equações e inequações logarítmicas, bem como para determinar o domínio das funções logarítmicas.

Consequências da definição

• log_b1 = 0
  log​_b​​1 = x → b​^x​​ = 1 → x = 0

• log​_b​​b = 1
  log​_b​​b = x → b^x = b¹ → x = 1

• b^{​log_​b​​a}​ ​= a
  Fazendo b^{​log​_b​​a ​}​= b​^x​​, temos que log​_b​​a = x e, da definição desse logaritmo, temos que b​^x ​​= a. Portanto: b​^log​​_ba​​ = b^x ​​= a

 Propriedades

Propriedade I

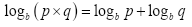
Propriedade II

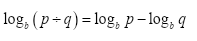
Propriedade III

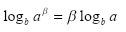
Propriedade IV

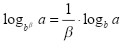
Proriedade V

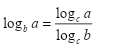
Cuidado! O número C é o número que você quiser.

Propriedade VI

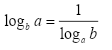
Propriedade VII