Questão de refração da UFRJ - Específica
Razão entre os índices de refração
Questão de refração da UFRJ
Questão de refração da UERJ
Questão de refração da UFF
Questão de refração do ITA
Questão de refração da FUVEST
Refração da Luz
A refração da luz consiste na passagem da luz de um meio para outro acompanhada de variação em sua velocidade de propagação. A refração pode ocorrer com ou sem desvio. Veja a figura:
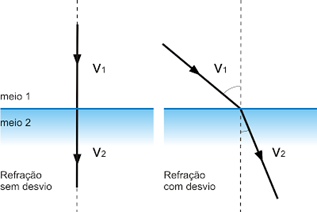
Índice de Refração Absoluto de um Meio para uma dada Luz Monocromática
Seja c a velocidade de propagação da luz no vácuo e v a velocidade de propagação de uma dada luz monocromática num determinado meio. A comparação entre c e v define a grandeza η, índice de refração absoluto:
η = c/v
Obs.:
- η é uma grandeza adimensional
- para os meios materiais, sendo c > v, resulta n > 1
- para o vácuo, n =1
- para o ar n ≈ 1
para um determinado meio material, temos para as diversas luzes monocromáticas:
ηvermelho < ηalaranjado < ηamarelo < ηverde < ηazul < ηanil < ηvioleta
Leis de Snell-Descartes
Observe a figura:
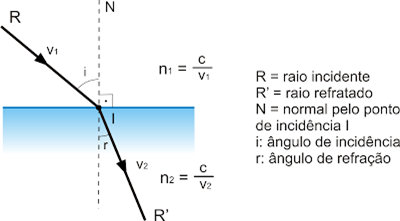
A lei de Snell-Descartes afirma que: é constante, na refração, o produto do índice de refração do meio pelo seno do ângulo que o raio forma com a normal à superfície de separação, neste meio.
Isto é:
η1 . sen(i) = η2 . sen(r)
Se η2 for maior do que η1, dizemos que o meio 2 é mais refringente do que o meio 1, resulta da lei de Snell-Descartes que sen(r) < sen(i) e, portanto, r < i.
Isto significa que: no meio mais refringente o raio de luz fica mais próximo da normal.
O mesmo é valido para p contrário. Se η2 for menor do que η1, dizemos que o meio 2 é menos refringente do que o meio 1, resulta da lei de Snell-Descartes que sen(r) > sen(i) e, portanto, r > i.