Probabilidade com exclusão
Probabilidade de um jogo
Continuação do exercício anterior
Soma de probabilidades
Probabilidade de raspadinha
Probabilidade condicional
Probabilidade do “ou”
Probabilidade de bolinhas numa caixa
Probabilidade
Experimento Aleatório: É todo aquele que o resultado é imprevisível como, por exemplo, o lançamento de um dado não viciado. Podemos lançar um dado n vezes mas ainda assim não podemos ter certeza do resultado.
Espaço Amostral: São todos os resultados possíveis do experimento aleatório. Esse conjunto é denotado por S ou Ω e também pode ser chamado como casos possíveis. No caso do dado S = {1, 2, 3, 4, 5, 6} que são as possibilidades de resultado de lançamento de um dado.
Evento: É qualquer subconjunto do espaço amostral. Quando calculamos probabilidade, estamos querendo saber a probabilidade do evento acontecer e é representado pela letra E . Também chamado de casos favoráveis. Por exemplo: Em um lançamento de dados, se o evento A forem os números pares então ele será: A = {2, 4, 6}
Dessa forma, podemos considerar que probabilidade de ocorrer o evento A é:
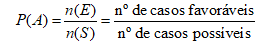
Ou seja, se quisermos saber a probabilidade de um lançamento de dado o número tirado ser ímpar, a resposta seria 3/6
É comum a resposta vir também como uma fração irredutível ou como porcentagem. No caso de 6/3, a fração irredutível seria 1/2 e em porcentagem seria 50%, dividindo 1 por 2 temos como resposta 0,5 ou seja 0,5 = 5/10 = 50/100 = 50%
Têm-se a probabilidade de 50% que o evento ocorra então temos 50% de que ele não ocorra, ou seja, do total 100% tiramos a probabilidade de o evento ocorrer e o resultado seria a probabilidade dele não ocorrer. Essa probabilidade é chamada de probabilidade complementar.
Definição
Chamamos de experimentos aleatórios aqueles que, repetidos em idênticas condições, produzem resultados diferentes. Embora não saibamos qual o resultado que irá ocorrer num experimento, em geral, conseguimos descrever o conjunto de todos os resultados possíveis que podem ocorrer. As variações de resultados, de experimento para experimento, são devidas a uma multiplicidade de causas que não podemos controlar, as quais denominamos acaso.
A probabilidade de um evento constituído por um certo número de elementos é a soma das probabilidades dos resultados individuais que constituem o evento A.
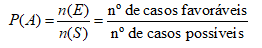
Sendo p a probabilidade, temos que, 0 ≤ p ≤1
Probabilidade complementar
Seja A um evento; então AC será também um evento que ocorrerá se, e somente se, A não ocorrer. Dizemos que AC é o evento complementar de A e calculamos, AC = 1 − P (A).