Questão de velocidade de propagação dos pontos de uma onda
Questão de refração da U.F.Viçosa
Questão sobre onda mecânica em diferentes meios da UFRJ
Questão de estados estacionários de uma onda
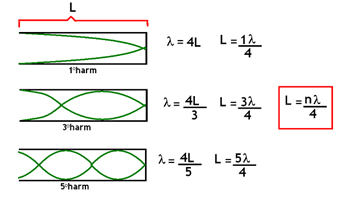
Questão de tubo fechado da Unirio
Questão de absorção de cores da UFRN
Questão de acústica da UFF
Questão de difração da UFRJ
Ondas periódicas
Ondas periódicas se caracterizam como uma sucessão regular de ondas, ou seja, o formato das ondas individuais se repete em intervalos de tempo iguais.
Vamos supor que temos uma corda com uma de suas extremidades fixa em uma parede e esticada por uma pessoa. Se fizermos o movimento da mão subindo e descendo, produziremos na corda uma perturbação, que vai se propagar ao longo da corda atéa extremidade fixa. Damos o nome àperturbação que se propaga no meio de pulso.
Se marcarmos um ponto colorido na corda e voltarmos a produzir uma perturbação nela, veremos que o ponto marcado permanece no mesmo lugar, porém o pulso se propaga atéchegar àoutra extremidade. Através dessa perturbação podemos ver que háapenas transferência de energia ao longo da corda. Não há transferência de matéria!
Sendo assim, podemos definir uma onda como sendo a propagação de energia de um ponto a outro, sem que haja transporte de matéria entre eles.
Ao estudarmos uma onda, podemos verificar que existem fontes que produzem ondas constantemente. Essas ondas produzidas em constância são denominadas ondas periódicas, ou seja, são ondas que se repetem com intervalos de tempos iguais. Na figura abaixo temos um exemplo básico de uma onda periódica se propagando em uma corda esticada.
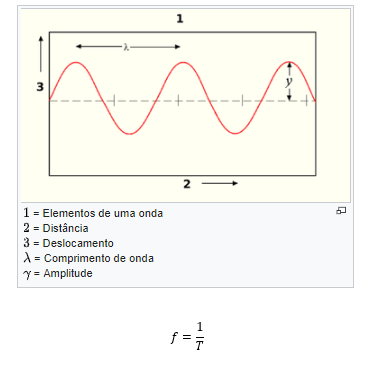
No sistema internacional de unidades (SI), a unidade de frequência éo hertz (Hz), que vale 1 Hz = s-1.
Comprimento de onda: representa a distância percorrida pela onda em um intervalo de tempo de um período. O comprimento de onda érepresentado pela letra (λ). Podemos ver na figura que o comprimento de onda corresponde àdistância entre duas cristas ou vales consecutivos.
A velocidade de propagação de uma periódica em um meio homogêneo éconsiderada uniforme e édeterminada pela seguinte equação:
v = △s/△t
Como, em um período, a onda desloca o equivalente a um comprimento de onda, então podemos escrever no lugar de Δs, λ; e no lugar de Δt, T. Reescrevendo a equação acima temos:
v = λ/T = λ.f
Acústica
Nessa aula vamos ficar em entender as qualidades físicas do som, ou seja, como podemos diferenciar determinados sons que podemos encontrar no nosso dia a dia.
As qualidades do som são diferenciadas a partir de:
Reflexão
Quando falamos de reflexão, estamos falando de um fenômeno ondulatório que vamos explicar com mais calma na aula de Fenômenos Ondulatórios, mas podemos comentar sobre algumas coisas aqui. A nível de qualidade do som, podemos observar que o som refletido consegue proporcionar dois fenômenos comuns no estudo sonoro: a Reverberação e o Eco.
O Eco acontece quando você emite um som, esse som reflete e você escuta o som refletido. No caso do Eco, você consegue notar a diferença entre o som emitido e o som refletido. A Reverberação tem o mesmo funcionamento do Eco, mas na reverberação você não consegue diferenciar o som emitido do refletido.
Timbre
O Timbre é a qualidade do som que te permite diferenciar sons de frequências iguais. É como se o Timbre fosse o "desenho" da onda. Se você pedir para alguém lança um “dó” em um violão e em uma flauta, apesar de ser a mesma nota, a capacidade que você tem de diferenciar o violão da flauto é através do Timbre.
Altura
Altura é a qualidade do som que se relaciona com a frequência. Apesar de ligarmos altura com intensidade (ex: Esse som ta muito alto!), para a Física, intensidade NÃO É a mesma coisa que altura. A altura de um som define se aquele som é um som Grave ou Agudo. Essa relação é feita da seguinte forma:
- Som Alto = Som Agudo
- Som Baixo = Som Grave)
Intensidade
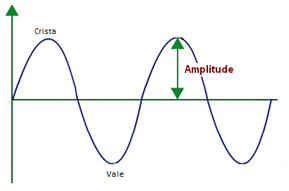
A intensidade é a qualidade do som que se relaciona com a amplitude da onda. Ou seja, quando falamos que uma onda é muito intensa, significa que ela tem uma amplitude muito grande. Lembre-se que Amplitude é a medida entre o meio de uma onda até a sua Crista ou Vale. Ondas muito intensas levam consigo muita energia.
Ondas estacionárias – Cordas vibrantes
O estudo de cordas vibrantes consiste na identificação de uma coisa: Harmônicos. No estudo de harmônicos nos relacionamos esses harmônicos com parâmetros ligados a onda, como comprimento de onda, frequência, etc. Ondas em corda de comprimento L, vamos analisar como são esses harmônicos.
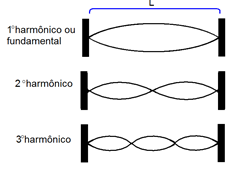
Na figura cima, pode-se deduzir uma fórmula para cálculo do comprimento de onda em função do comprimento da corda:
L = n . λ/2
Onde:
- n é o número do harmônico.
- L é o comprimento da corda.
- λ é o comprimento de onda.
Dica: Não é preciso decorar a fórmula se você perceber que o número do harmônico representa o número de “quibes” (metade do comprimento de onda) do desenho.
Ventre e Nó
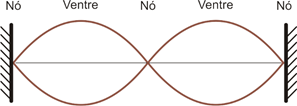
Em cordas vibrantes (e em tubos sonoros nas próximas aulas) nós podemos analisar pontos importantes em relação a interferência entre a onda emitida e a onda refletida. Esses pontos recebem o nome de Ventre e Nó. O Ventre é o ponto da onda onde ocorre interferência construtiva, ou seja, esse ponto onde a intensidade apresenta seu maior valor. Já o Nó é o ponto da onda onde ocorre a interferência destrutiva, ou seja, esse ponto onde a intensidade assume um valor nulo.
Ondas estacionárias – Tubos
- aberto: forma ventre
- fechado: forma nó
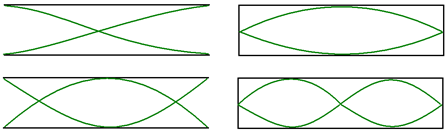
A fórmula é a mesma da onda estacionária em corda (e o raciocínio dos harmônicos também). O tubo que é fechado em uma extremidade e aberto na outra possui apenas os harmônicos ímpares.