Exercícios sobre lentes em Física

Lentes Esféricas

As lentes são os sistemas ópticos de maior importância em nossa civilização. São componentes tanto de um simples par de óculos quanto de uma sofisticada máquina de filmar ou de um complexo microscópio.

Uma lente esférica modifica a direção dos raios de luz. Uma lente é construída com um material homogêneo e transparente. Em geral, o material que “envolve” a lente é o mesmo. Nos casos que estudaremos juntos, é o ar.

Um uso bastante comum das lentes é feito para fazer a correção de defeitos da visão, como miopia, hipermetropia e astigmatismo. Até mesmo o nosso olho funciona de modo semelhante a uma lente.

Como a lus deve atravessar as duas interfaces da lente, uma vez ao incidir na lente e outra ao emergir da lnte, ocorrem duas refrações. Essas refrações podem produzir imagens ampliadas ou reduzidas e sem grandes deformações das imagens.

Adiante, para simplificar as situações, consideraremos o ar como o meio externo às lentes. Vale ressaltar que as lentes são normalmente constituídas de vidro, acrílico ou cristal.

1. Classificação das lentes

As lentes podem ter bordas finas ou espessas, podendo a face ser plana, côncava ou convexa. A seguir temos diferentes tipos de lentes:

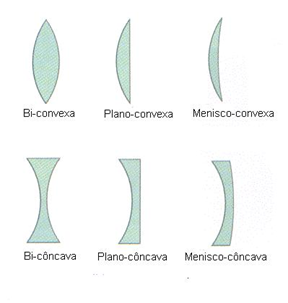
As seis lentes apresentadas na figura acima são divididas em dois grupos: lentes de bordas finas (sendo essas as três na parte superior da figura) e lentes de bordas espesas (essas na parte inferior da figura).

1.1 Classificação quanto ao desvio de luz

Uma lente pode ser convergente ou divergente. Essa classificação depende da relação entre o índice de refração da lente (n1) e o índice de refração do meio (nmeio).

• Quando o índice de refração da lente é maior do que o do meio no qual ela está imersa (n1 > nmeio), as lentes de bordas finas são convergentes. Essa é a situação mais comum de ser encontrada, visto que geralmente as lentes analisadas encontram-se no ar.
• Quando o índice de refração da lente é menor do que o do meio no qual ela está imersa (n1 < nmeio), as lentes de bordas finas são divergentes e as lentes de bordas grossas são convergentes.

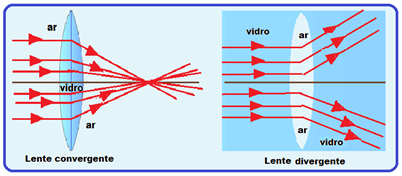
Raios Luminosos

Na figura a seguir tem-se representado como os raios luminos se comportam nos dois diferentes tipos de lentes:

Principais elementos de uma lente

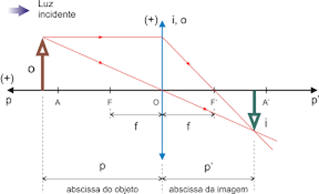
A seguir, estarão apresentados alguns elementos importantes no estudo das lentes delgadas, sendo essas cujas as lentes esféricas muito pequenas (desprezível):

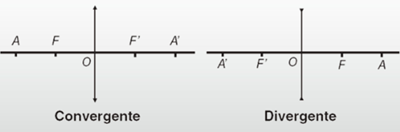
Onde:

• O – centro óptico da lente;
• F – foco principal do objeto;
• F’ – foco principal da imagem;
• AF = FO = OF’ = F'A = f − distância focal;
• A – ponto antiprincipal objeto, definido tal que AO = 2f;
• A’ – ponto antiprincipal imagem, definido tal que A'O = 2f.

Raios Principais nas lentes

Incidência sobre o fofo principal objeto

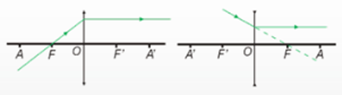
Incidência paralela ao eixo principal

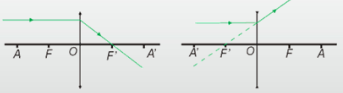
Incidência sobre o centro óptico

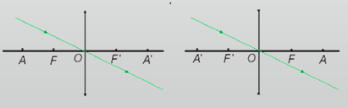
Construção de imagens

A construção de imagens nas lentes esféricas é semelhante à dos espelhos esféricos e depende da posição do objeto em relação à lente.

1. Lentes convergentes

Um ponto muito importante a ser observado é que as lentes convergentes formam imagens com iguais classificações que os espelhos côncavos.

i. Objeto situado antes do ponto antiprincipal objeto (A): a imagem é real e, em relação ao objeto, menor e invertida

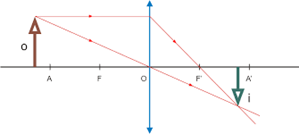
ii. Objeto situado sobre o ponto antiprincipal objeto (A): a imagem é real e, em relação ao objeto, tem o mesmo tamanho e é invertida.

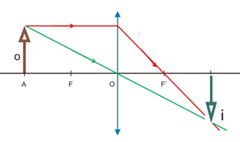
iii. Objeto situado entre o ponto antiprincipal objeto (A) e o foco objeto (F): a imagem é real e, em relação ao objeto, é maior e invertida.

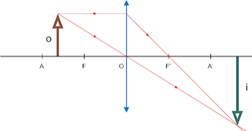
iv. Objeto situado sobre o foco objeto (F): a imagem é imprópria.

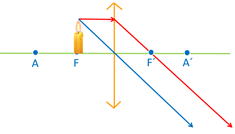
v. Objeto situado entre o foco objeto (F) e o centro óptico (O): o imagem é virtual e, em relação ao objeto, meior e direita.

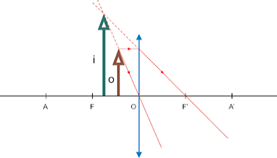
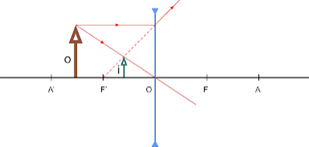
2. Lentes Divergentes

A lente é sempre virtual e, em relação ao objeto, é direita e menor.

Equação de Gauss

A equação de Gauss relaciona a posição do objeto (p) com a posição da imagem (p’) e a distância focal da lente (f).

1/f = 1/p + 1/p'

Analisando os sinais dos variáveis na expressão acima:

• p e p’ positivos: posição do objeto antes da lente e posição da imagem depois da lente;
• p e p’ negativos: posição do objeto depois da lente e posição da imagem antes da lente;
• f > 0: lente convergente;
• f < 0: lente divergente.

Aumento Linear

A equação a seguir permite relacionar o comprimento do objeto e da imagem (perpendicular em relação ao eixo principal da lente) e as distâncias do objeto e da imagem à lente.

A = i/o = -p'/p

• i e o positivos: imagem e objeto direitos;
• i e o negativos: imagem e objeto invertidos.