Questão de Magnetismo da PUC
Exercício de produto vetorial entre VxB ( regra da mão esquerda)
Questão de Magnetismo da UFF
Questão de Magnetismo da UFRJ
Questão de Magnetismo da UFRJ
Questão de Magnetismo da FUVEST
Questão de Magnetismo da UFRN
Questão de Magnetismo da UFRJ
Ímãs e magnetos
Um ímã é definido com um objeto capaz de provocar um campo magnético à sua volta. Podendo ser ele natural ou artificial.

Figura 01 – Imã natural Figura 02 - Imã artificial
Um ímã natural é feito de minerais com substâncias magnéticas, como por exemplo, a magnetita. Já o ímã artificial é feito de um material sem propriedades magnéticas, mas que pode adquirir permanente ou instantaneamente características de um ímã natural.
Os ímãs artificiais também são subdivididos em: permanentes ou temporais:
- Um ímã permanente é feito de material capaz de manter as propriedades magnéticas mesmo após cessar o processo de imantação, estes materiais são chamados ferromagnéticos.
- Um ímã temporal tem propriedades magnéticas apenas enquanto se encontra sob ação de outro campo magnético, os materiais que possibilitam este tipo de processo são chamados paramagnéticos.
Polos magnéticos
São as regiões onde se intensificam as ações magnéticas. Um ímã é composto por dois polos magnéticos, norte e sul, normalmente localizados em suas extremidades, exceto quando estas não existirem, como em um ímã em forma de disco, por exemplo. Por esta razão são chamados dipolos magnéticos.

Figura 03 – Dipolos magnéticos
Para que sejam determinados estes polos, se deve suspender o ímã pelo centro de massa e ele se alinhará aproximadamente ao polo norte e sul geográfico recebendo nomenclatura equivalente. Desta forma, o polo norte magnético deve apontar para o polo norte geográfico e o polo sul magnético para o polo sul geográfico (vamos nos aprofundar nisso durante o resumo).
Atração e repulsão
Ao manusear dois ímãs percebemos claramente que existem duas formas de colocá-los para que estes sejam repelidos e duas formas para que sejam atraídos. Isto se deve ao fato de que polos com mesmo nome se repelem, mas polos com nomes diferentes se atraem, ou seja:
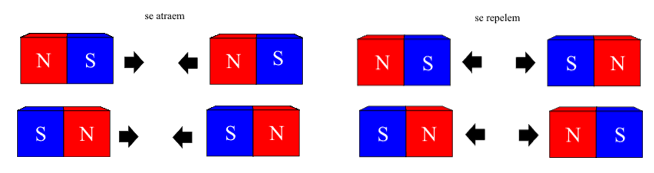
Figura 04 - Atração de imãs Figura 05 - Repulsão de imãs
Esta propriedade nos leva a concluir que os polos norte e sul geográficos não coincidem com os polos norte e sul magnéticos. Na verdade eles se encontram em pontos praticamente opostos, como mostra a figura abaixo:
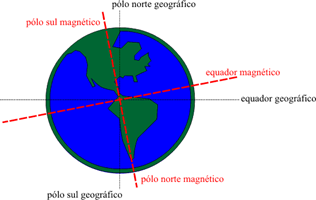
Figura 06 – Polos magnéticos terrestres
A inclinação dos eixos magnéticos em relação aos eixos geográficos é de aproximadamente 191°, fazendo com os seus polos sejam praticamente invertidos em relação aos polos geográficos.
Interação entre polos
Dois polos se atraem ou se repelem, dependendo de suas características, à razão inversa do quadrado da distância entre eles. Ou seja, se uma força de interação F é estabelecida a uma distância d, ao dobrarmos esta distância a força observada será igual a uma quarta parte da anterior F/4. E assim sucessivamente.
Inseparabilidade dos polos de um ímã
Esta propriedade diz que é impossível separar os polos magnéticos de um ímã, já que toda vez que este for dividido serão obtidos novos polos, então se diz que qualquer novo pedaço continuará sendo um dipolo magnético.
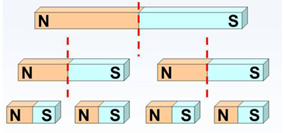
Figura 07 – Inseparabilidade dos polos
Campo Magnético
É a região próxima a um ímã que influencia outros ímãs ou materiais ferromagnéticos e paramagnéticos, como cobalto e ferro. Compare campo magnético com campo gravitacional ou campo elétrico e verá que todos estes têm as características equivalentes.
Também é possível definir um vetor que descreva este campo, chamado vetor indução magnética e simbolizado por \vec BB⃗. Se pudermos colocar uma pequena bússola em um ponto sob ação do campo o vetor \vec BB⃗ terá direção da reta em que a agulha se alinha e sentido para onde aponta o polo norte magnético da agulha.
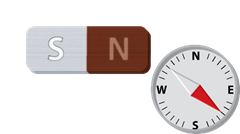
Figura 08 – Relação imã/bússola
Se pudermos traçar todos os pontos onde há um vetor indução magnética associado veremos linhas que são chamadas linhas de indução do campo magnético. estas são orientados do polo norte em direção ao sul, e em cada ponto o vetor \vec BB⃗ tangencia estas linhas.
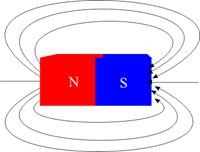
Figura 09 – Campo magnético
As linhas de indução existem também no interior do ímã, portanto são linhas fechadas e sua orientação interna é do polo sul ao polo norte. Assim como as linhas de força, as linhas de indução não podem se cruzar e são mais densas onde o campo é mais intenso.
Campo Magnético Uniforme
De maneira análoga ao campo elétrico uniforme, é definido como o campo ou parte dele onde o vetor indução magnética \vec BB⃗ é igual em todos os pontos, ou seja, tem mesmo módulo, direção e sentido. Assim sua representação por meio de linha de indução é feita por linhas paralelas e igualmente espaçadas.
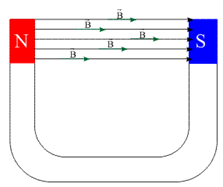
Figura 10 – Campo magnético Uniforme
Força magnética
Força magnética sobre uma partícula eletrizada lançada num campo magnético uniforme
Como já vimos, portadores de carga elétrica em movimento geram campo magnético. Se o movimento da partícula ocorre num campo magnético uniforme, teremos a interação desses campos se manifestando através de uma força magnética.
Figura 11 – Vetor força magnética
Força magnética F que age numa partícula eletrizada com carga elétrica q lançada com velocidade v num campo magnético B. Essa força magnética (Força de Lorentz) é calculada por:
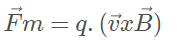
Onde o símbolo ”x” significa produto vetorial. Não é uma multiplicação!
- Módulo 🡪 Fm = |q|.v.B.senθ
- Direção 🡪 Perpendicular ao plano determinado pelos vetores B e v.
- Sentido 🡪 Determinado pela “regra da mão direita” (também tem a “regra da mão esquerda”).
Como foi dito, para encontrar o vetor força magnética a partir dos vetores campo magnético e velocidade, vamos utilizar a regra da mão esquerda ou a regra da mão direita (escolha qual você preferir).
Regra da mão esquerda
Figura 12 - regra da mão esquerda
O sentido da força magnética pode também ser determinado pela regra da mão esquerda. Veja a figura abaixo. O dedo polegar fornece o sentido da força magnética considerando q > 0. Para q < 0, o sentido da força magnética é oposto.
1) Partícula eletrizada com carga q > 0 lançada paralelamente às linhas de indução magnética do campo (V//B).
Figura 13 – Velocidade paralela ao campo magnético
Sendo:
Fm = |q|.v.B.senθ
e
θ = 0° ou θ = 180°, em ambos os casos senθ = 0.
Sendo assim:
Fm = 0, temos então, um movimento retilíneo uniforme MRU.
2) Partícula eletrizada com carga q>0 lançada perpendicularmente às linhas de indução magnética do campo (V_|_B).
Figura 14 – Velocidade perpendicular ao campo magnético
Sendo
Fm = q.v.B.senθ
e
θ=90°, temos sen90°=1.
Sendo assim:
Fm = q.v.B
Atenção!
Sendo Fm perpendicular à v ao longo de todo o movimento, esta força tem sua atuação como resultante centrípeta, não variando o módulo da velocidade, mas somente sua direção, obrigando a partícula eletrizada à realizar um movimento circular uniforme (MCU).
Fm = Rcentrípeta
v / B 🡪 MCU
3) Partícula eletrizada com carga q>0 lançada obliquamente às linhas de indução magnética do campo.
Figura 15 - Velocidade oblíqua ao campo magnético
Neste caso, decompomos a velocidade de lançamento v nas componentes: v1(paralela a B) e v2 (perpendicular a B). Devido a v1 a partícula descreve um MRU e devido a v2, um MCU. A composição de um MRU com um MCU resulta em um movimento uniforme com trajetória helicoidal.