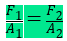Questão de pressão
Questão de vasos comunicantes
Questão de vasos comunicantes com conversão de unidades
Questão de pressão hidrostática
Questão de prensa hidráulica
Questão de equilíbrio de um corpo
Questão de empuxo
Questão de pressão total em um mergulhador
Questão teórica de empuxo
Questão de um corpo emerso
Questão de tração de um corpo submerso
Questão de fluidoestática
Massa Específica ou Densidade
Sejam m1, m2, ..., mn as massas de porções de uma substância pura em uma mesma temperatura e submetida à mesma pressão. Sendo V1, V2, ..., Vn os respectivos volumes, podemos verificar que:
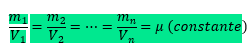
Por definição, a constante m é a massa específica ou densidade absoluta da substância.
Do exposto, concluímos que: Em pressão e temperatura constantes, uma substância pura tem massa específica (m) constante e calculada pela divisão da massa considerada (m) pelo volume correspondente (V):
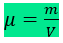
Unidade SI: Kg/m³
Densidade do corpo (d)
Por definição, a densidade de um corpo (d) é o quociente de sua massa (m) pelo volume delimitado por sua superfície externa (Vext):
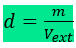
Pressão
É a grandeza escalar que corresponde à razão entre a resultante perpendicular (normal) das forças e sua área de atuação.
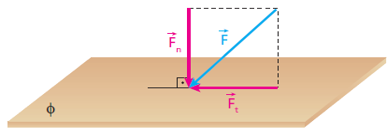
Figura 01 - Pressão. Fonte: Tópicos de Física - Vol. 1 - 21ª Ed 2012
Por definição, a pressão média (pm) que F exerce na superfície φ é obtida dividindo-se o módulo da componente normal de F em relação a f (Fn) pela correspondente área A:
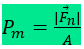
Unidade (SI): N/m² = Pa (Pascal)
Teorema de Stevin
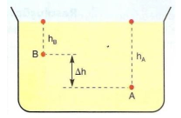 Figura 02 - Lei de Stevin. Fonte: Tópicos de Física - Vol. 1 - 21ª Ed 2012
Figura 02 - Lei de Stevin. Fonte: Tópicos de Física - Vol. 1 - 21ª Ed 2012
Consideremos um líquido de massa específica μ, em equilíbrio no recipiente da figura. Os pontos A e B do líquido estão situados a uma distância hA e hB, respectivamente, da superfície do líquido.
Pode-se mostrar que:
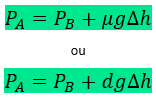
Princípio de Pascal
O Princípio de Pascal enuncia-se da seguinte forma:
“A diferença de pressão entre dois pontos de um flúido homogêneo em equilíbrio é constante, dependendo apenas do desnível entre esses pontos. Logo, se produzirmos uma variação de pressão num ponto de um flúido em equilíbrio, essa variação se transmite a todo o flúido”
ou seja, todos os pontos do fluido sofrem a mesma variação de pressão. Uma aplicação prática é a prensa hidráulica.
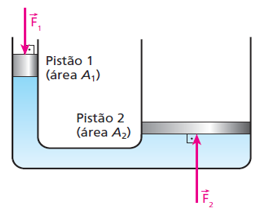 Figura 3 – Princípio de Pascal. Fonte: Tópicos de Física – Vol.1 – 21ª Ed. 2012.
Figura 3 – Princípio de Pascal. Fonte: Tópicos de Física – Vol.1 – 21ª Ed. 2012.
Assim, se F1 e F2 são as magnitudes das forças sobre os pistões de áreas A1 e A2, respectivamente, temos:
Princípio de Arquimedes
Consideremos um corpo sólido cilíndrico circular, de área da base A e altura h, totalmente imerso num fluido em equilíbrio, cuja densidade é d (Figura 4). Por simetria, vemos que as forças sobre a superfície lateral do cilindro se equilibram duas a duas [pressões (p, p) e (p´,p´) na figura]. Entretanto, a pressão p2 exercida pelo fluido sobre a base inferior é maior do que a pressão p1 sobre a base superior. Pelo teorema de Stevin:
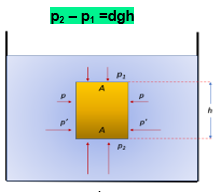
Figuro 4: Princípio de Arquimedes
Logo, a resultante das forças superficiais exercidas pelo fluido sobre o cilindro será uma força vertical , dirigida para cima, com:
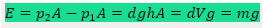
Onde E é o empuxo, dado por: E = dVg