Exercício sobre definição de grandezas diretas e inversas
Exercício sobre relação entre grandezas proporcionais
Exercício sobre divisão inversamente proporcional
Exercício sobre divisão diretamente proporcional
Exercício sobre escala
Exercício sobre escala envolvendo área
Exercício sobre escala volumétrica
Exercício sobre grandezas proporcionais com fórmula
Grandezas Proporcionais e Escala
Razões e proporções
Razão é a fração determinada por duas grandezas, que visa a obter a relação que se estabelece entre as quantidades de cada uma delas em uma determinada situação. Assim, uma razão entre as grandezas a e b é dada por a/b
Quando duas razões têm o mesmo resultado, ou seja, se elas são iguais, determinam uma proporção. Desse modo, a proporção dada por quatro números a, b, c e d é representada pela seguinte igualdade de razões:
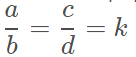
em que k é a constante de proporcionalidade
Grandezas Diretamente Proporcionais
Duas grandezas a e b são diretamente proporcionais quando a razão entre elas é constante, ou seja:

Assim, ao variar uma grandeza, a outra também varia na mesma razão.
Exemplo: Um pai deixou para seus filhos André, Bruno e Cristiano uma herança de R$ 70.000,00 a ser distribuída em quantias diretamente proporcionais a 1,2 e 4, respectivamente. Quanto cada um dos três filhos recebeu?
Chamemos por A, B e C as quantias recebidas por André, Bruno e Cristiano, respectivamente. A seguinte proporção pode ser montada:
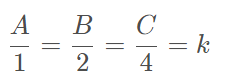
Igualando-se cada razão à constante k de proporcionalidade, podem-se criar as seguintes equações:
A = k , b = 2k e C = 4K
Dessa maneira, sabemos que a soma das quantias recebidas por cada um é o valor total da herança, R$ 70.000,00
A + B + C = 70000
k + 2k + 4k + 70000
7k + 70000
k = 10000
Assim, André recebeu R$ 10 000,00, Bruno recebeu R$ 20 000,00 e Cristiano, R$ 40 000,00.
Grandezas Inversamente proporcionais
Duas grandezas a e b são diretamente proporcionais quando o produto entre elas é constante, ou seja:
a.b = k
Assim, ao variar uma grandeza, a outra também varia na razão inversa.
Exemplo: Um pai deixou para seus filhos André, Bruno e Cristiano uma herança de R$ 70.000,00 a ser
distribuída em quantias inversamente proporcionais a 1, 2 e 4, respectivamente. Quanto cada um dos três filhos recebeu?
Chamemos por A, B e C as quantias recebidas por André, Bruno e Cristiano, respectivamente.
A seguinte proporção pode ser montada:
A = 2B = 4C = k
Igualando-se cada razão à constante k de proporcionalidade, podem-se criar as seguintes equações:
A = k, B = k/2 e C = k/4
Dessa maneira, sabemos que a soma das quantias recebidas por cada um é o valor total da herança, R$ 70.000,00:
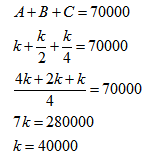
Assim, André recebeu R$ 40 000,00, Bruno recebeu R$ 20 000,00 e Cristiano, R$ 10 000,00.
Escala
Escalas de mapas e miniaturas são exemplos de razões entre grandezas de mesma natureza (neste caso, comprimento). Uma escala (e) é a razão entre o comprimento do desenho ou da miniatura (d) e o comprimento real.

Escalas de mapas e miniaturas geralmente são representadas na forma de 1 : R , ou seja, 1 unidade de comprimento do desenho representa R unidades de comprimento no real. Existem também escalas de áreas, que é o valor da escala ao quadrado, e escalas volumétricas, que é o valor da escala ao cubo.