Exercício envolvendo centro, raio e foco
Questão de espelho côncavo da UFF
Questão de espelho côncavo e convexo da UFRN
Questão de espelho côncavo da UFRN
Questão de espelhos planos, côncavos e convexos da UFF
Questão de espelhos esféricos da UERJ
Espelhos Esféricos
Para o estudo dos espelhos esféricos, precisamos de algumas definições.
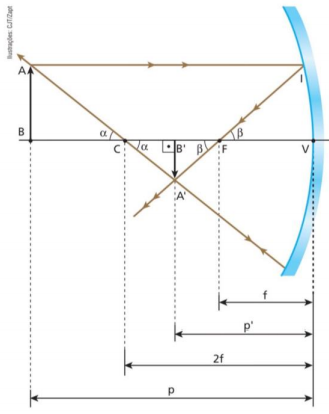
De acordo com a imagem, podemos definir:
P = distância entro o objeto e o espelho
P' = distância entre a imagem e o espelho
f = distância focal
Apesar de não existir, encontraremos distâncias positivas e negativas nesse estudo. Os valores positivos e negativos não estão atrelados à distância em si, mas à posição em relação ao espelho.
Logo, faremos uso desses sinais para classificar espelhos, objetos e imagens de acordo com o que foi visto no modulo anterior.
- f > 0 significa que o espelho é côncavo
- f < 0 significa que o espelho é convexo
- P > 0 significa que o objeto é real
- P < 0 significa que o objeto é virtual
- P' > 0 significa que a imagem é real
- P' < 0 significa que a imagem é virtual
Obs: Preste atenção por que algumas questões podem lhe dar os valores e uma figura demonstrando a situação. Nesse caso, cabe a você atraibuir os sinais positivos e negativos às medidas.
Com essas grandezas bem definidas, podemos introduzir a equação de Gauss, que relaciona a distância focal e as distâncias do objeto e da imagem ao:

Aumento linear transversal
O aumento linear é uma grandeza relacionada à imagem, e representa o aumento que essa imagem pode ter. Se você olhar a imagem abaixo pode notar que ela representa um raio notável que passa pelo objeto e forma a imagem.
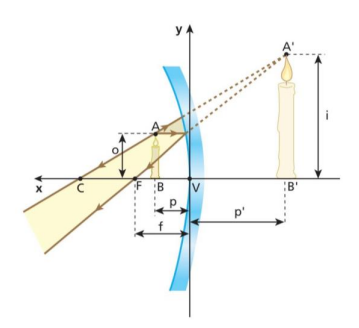
Podemos notar que existem dois triângulos sendo formados graças a esse raio notável e eles podem ser relacionados, definindo o aumento linear como:
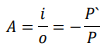
Esse “-“ faz parte de uma correção na formula. Para definir o tamanho das imagens, faremos uso do sistema de coordenadas, estrategicamente, localizado no vértice do espelho, conforme a imagem a cima. Assim, definimos valores positivos para objetos e imagens com orientação positiva do eixo y e negativo para imagens e objetos invertidos. Essa relação pode ser observada no valor final do aumento linear da seguinte forma:
- A < 0 significa que a imagem é invertida em relação ao objeto
- A > 0 significa que a aimagem é direita em relação ao objeto
Obs.: Lembra-se que essa classificação é em relação ao objeto. Se tanto o objeto quanto a aimagem estiverem para baixo, o valor de A será positivo e vie-versa.