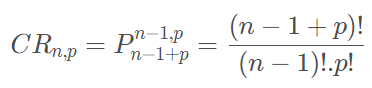Exercício sobre Cores
Exercícios sobre PFC e Permutação
Exercício sobre Sorteio de times
Questão sobre intervalos na reta dos reais
Exercício sobre museus
Exercício sobre cores de uma casa
Exercício sobre braille
Exercício sobre espécies
Análise Combinatória
Fatorial
O fatorial é uma operação aplicada apenas a número naturais e é definido da seguinte maneira: ∀m ∈ N temos:
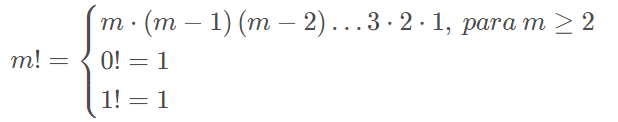
Princípio Fundamental da Contagem (PFC)
Essa técnica básica de contagem visa calcular o número de possibilidades de ocorrência de um evento E, composto por uma série de sub-eventos independentes: E1, E2, E3… Na composição do evento E, escolhe-se apenas umas das possibilidades de cada um de seus sub-eventos.
Representamos os totais de possibilidades pelas quais os eventos podem ocorrer por:
n(E): número de possibilidades do evento E
n(Ei): número de possibilidades do evento Ei
Podemos enunciar que o número de possibilidades de ocorrência do evento E é dado por:
n(E) = n(E)1.n(E)2…n(E)n
Permutações
Permutação simples de n objetos distintos
Dado um conjunto com n elementos distintos, chama-se permutação dos n elementos, todo arranjo desses n elementos tomados n a n
P = n!
Permutação com elementos repetidos
De modo geral, se temos n elementos dos quais n1 são iguais a a1, n2 são iguais a a2, n3 são iguais a a3 , … , nr são iguais a ar, o número de permutações possíveis é dado por:
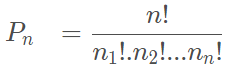
Arranjo
Dado um conjunto com n elementos distintos, chama-se arranjo dos n elementos, tomados p a p, a qualquer sequência ordenada de p elementos distintos escolhidos entre os n existentes.
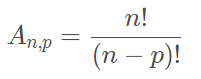
Combinação Simples
Número de combinações de n elementos tomados p a p onde a ordem não importa
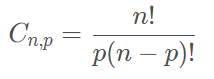
Permutação Circular
Permutação circular é um tipo de permutação composta por n elementos distintos em ordem cíclica (formando uma circunferência).
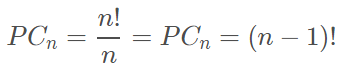
Combinações Completas
Combinações completas de n elementos, tomados p a p, são combinações de n elementos não necessariamente distintos. Em vista disso, quando vamos calcular as combinações completas devemos levar em consideração as combinações com elementos distintos (combinações simples) e as combinações com elementos repetidos.