Exercícios sobre Conjuntos Numéricos em Matemática

Conjunto dos Números Naturais

O primeiro conjunto numérico a ser estudado é o conjunto dos naturais, representados por “N” que surgiu a partir do momento que foi sentido a necessidade da contagem de elementos.

N = {0, 1, 2, 4, 5, 6, …}
N* = {1, 2, 3, 4, 5, 6, …}

Obs.: A notação “*” simboliza o conjunto sem o elemento nulo(zero).

Adição de números naturais

Essa é uma operação fechada no conjunto dos naturais, ou seja, a adição de dois números naturais resulta em um número natural.

Exemplo: 17 + 8 = 25, ou seja, somando dois naturais, resultado natural.

Propriedades

• Associativa: (a + b) + c = a + (b + c) = b + (a + c)
• Comutativa: a + b = b + a
• Elemento Neutro: O zero é o elemento neutro da adição pois ao somarmos zero, o resultado não se altera.

Multiplicação de números naturais

A multiplicação no conjunto dos naturais também é uma operação fechada pois na multiplicação de quaisquer dois naturais, o resultado também é natural.

Exemplo: 15 x 8 = 120, ou seja, multiplicando dois naturais, resultado natural.

Propriedades

• Comutativa: a . b = b . a
• Associativa: (a . b) . c = a . (b . c) = b . (a . c)
• Distributiva: a . (b + c) = ab + ac e a.(b – c) = ab - ac
• Elemento Neutro: O elemento neutro da multiplicação é o um pois ao multiplicarmos um número por um, o resultado não se altera.

Divisão de números naturais

Na divisão de números naturais, nem todos os resultados são naturais.

Exemplos: 15 : 5 = 3, porém, 7 : 2 = 3,5 e 3,5 não é natural.

Conjunto dos Números Inteiros

O conjunto dos números inteiros, representado por “Z”, surgiu a partir do momento que surgiu a ideia de dívida, assim, entrando os números negativos.

Z = {…, -3, -2, -1, 0, 1, 2, 3, …}

Alguns subconjuntos são destacáveis:

Operações com Inteiros

As operações com números inteiros funcionam como no conjunto dos naturais. O que difere os inteiros são os números negativos, assim, entramos com a propriedade dos números opostos.

Exemplo: O oposto de 3 = (-1) . 3 = -3 ; O oposto de -4 = (-1) . (-4) = 4.

Conjunto dos Números Racionais

O conjunto dos racionais surgiram quando houve necessidade de representar uma parte de um inteiro e é todo número da forma a/b, com b ≠ 0. Ou seja, são razões (quocientes) entre dois números inteiros. A definição formal é:

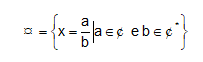
Obs: Lembrando que entre dois números racionais há infinitos números racionais.

Obs 2: Dízimas periódicas são racionais pois podem ser escritas sob a forma de fração.

Operações com Racionais

Com os números racionais, além das propriedades já vistas, adicionamos a propriedade do inverso de um número.

Exemplo: O inverso de 4 ​ = ¼

Operações entre frações

Soma e subtração

Caso os denominadores sejam iguais, bastar somar os numeradores e repetir o denominador.

Multiplicação

Multiplica-se numerador com numerador e denominador com denominador, simplificando, se possível, o resultado

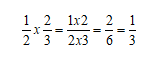
Divisão

Repete a primeira fração e multiplica pelo inverso da segunda fração.

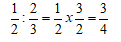
Dízima periódica

Número decimal que possui uma repetição periódica e infinita de termos (período) , mas não tem uma representação exata. São classificadas como simples e compostas:

• Simples: o período começa logo após a vírgula. Exemplo: 0,3333… , 0,121212… e 1,3333…
• Composta: Existe uma parte não periódica entre a virgula e o período: Exemplo: 0,0222…, 1,125555…
  
  

Conjunto dos Números Irracionais 

Os números irracionais são números que não podem ser escritos sob a forma de fração pois são números decimais infinitos e não periódicos.Como exemplos de números irracionais podemos ter:

• π
• √2 ≈ 1,414213562…
• √5 ≈ 2,236067977…

 
Operações com Irracionais

Como os números irracionais são números infinitos e não periódicos, não os representamos como decimais. Assim, normalmente não efetuamos operações com números irracionais, os deixando indicados quando isso ocorre.

Exemplo: 1+√2 é uma soma que deixamos indicados por não conseguir somar ao certo esses valores.

Conjunto dos Números Reais 

Os números reais, representados por R é a união dos conjuntos dos Racionais com os Irracionais. Ou seja: