Estudo dos polígonos em Matemática

Estudo dos polígonos

Definição

Polígono é uma linha fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano.

Polígonos e não-convexos

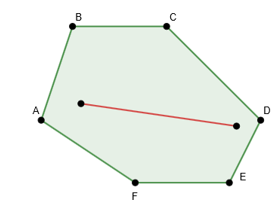
O polígono ABCDEF é convexo, pois se tomarmos dois pontos quaisquer na região limitada pelo polígono, o segmento de reta que os une sempre estará inteiramente contido nesta região. Uma outra maneira de visualizar se um polígono é convexo ou não, é pelas diagonais: se um diagonal passar por fora do polígono, então ele é côncavo.

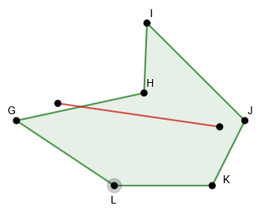
O polígono GHIJKL é não-convexo, por não cumprir a regra do convexo. Vemos, também, que a diagonal não está contida no interior do polígono.

Elementos de um polígono convexo

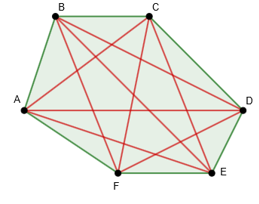
Um polígono convexo tem alguns elementos importantes a ser estudados como: vértices, lados, diagonais, ângulos internos e ângulos externos.

Vértices
São os pontos A, B, C, D, E e F.

Lados
São os segmentos de reta AB, BC, CD, DE, EF e FA .

Diagonais
São os segmentos de reta que ligam um vértice a outro não consecutivo a ele: AC, AD, AE, BD, BE, BF, CE, CF e DF.
Para encontrar o número de diagonais que um polígono possui, basta calcular pela fórmula:

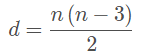
Ângulos Internos
São formados por dois lados consecutivos contidos na região interna do polígono: ABC ou B, BCD ou C, CDE ou D, DEF ou E, DFA ou F e FAB ou A .

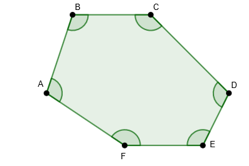
A soma dos ângulos internos é dada pela fórmula:

Onde n é o número de lados do polígono.
 
Ângulos Externos

São os ângulos formados por um lado e pelo prolongamento do lado consecutivo a este

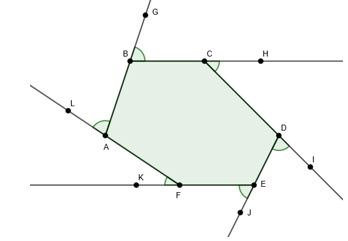
A soma dos ângulos externos é sempre 360º, qualquer que seja o polígono

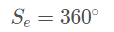
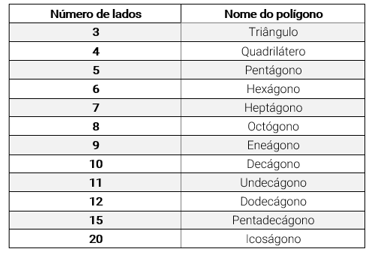
Nome dos polígonos quanto ao número de lados