Estatística em Matemática

Resumo

O tratamento da Informação engloba a leitura de gráficos e tabelas simples. Vamos estudá-los!

Gráficos

Gráfico de Setores

O gráfico de setores é feito por uma circunferência vejamos o exemplo a seguir:

Ex.: Em um campeonato foram registrados quantos pontos cada equipe fez durante todo o campeonato, e foi apresentado no gráfico de setores a seguir:

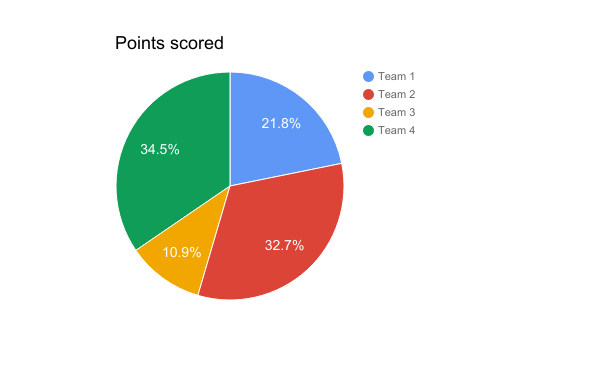
Temos então que a Equipe 1 marcou 21,8% dos pontos, Equipe 2, 32.7%, Equipe 3, 10,9% e Equipe 4, 34,5%.

Podemos então observar que a equipe que mais marcou pontos foi a Equipe 4.

OBS.: Mais precisamente, as medidas dos ângulos dos setores circulares são proporcionais às porcentagens de ocorrência das realizações das variáveis. Em outra palavras, podemos usar regra de três para encontrá-lo.

Gráfico de Barras

Temos a seguir o gráfico de barras, também falando das equipes em um campeonato.

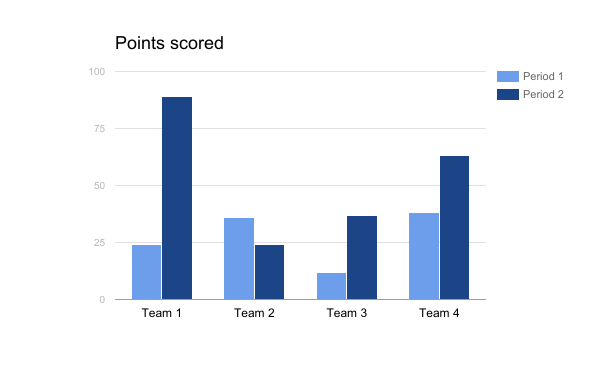
O gráfico é dividido em dois períodos e mostra como que cada equipe se saiu.

Com esse gráfico podemos tirar algumas informações:

→ A equipe 1 teve a maior melhora desde o período 1 para o 2.

→ A equipe 3 teve o pior período 1.

→ Muitas informações podem ser tiradas, basta observar e comparar.

Gráfico de Linhas

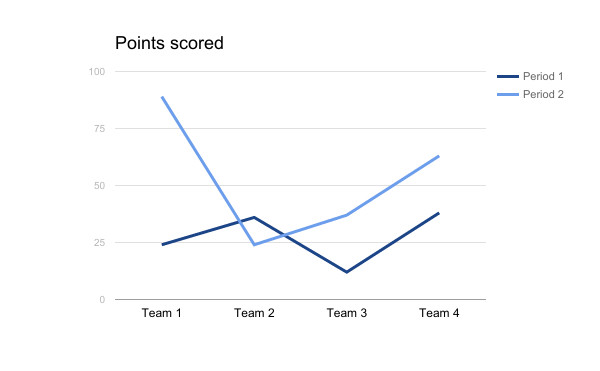
O uso dessa representação gráfica é útil quando se quer representar valores assumidos por uma grandeza, no decorrer do tempo.

Tabelas de Frequência

 A organização dos dados em tabelas possibilita uma leitura rápida e resumida dos resultados obtidos em uma pesquisa.Para cada variável estudada, contamos o número de vezes que cada um de seus valores (de realizações) acontece. O número obtido é chamado de frequência absoluta.

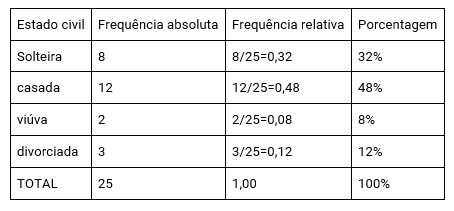
 Ex.: Foi feita uma pesquisa com mulheres e seus respectivos estados civis.

Em Estatística, medidas de centralidade são usadas para representar toda uma lista de observações com um único valor. Já as medidas de dispersão mostram o quão esticada ou espremida está uma distribuição de observações.

 Medidas de centralidade:

 1) Média:

1.1) Média aritmética simples:

A média aritmética simples de um conjunto {x1, x2, ..., xn} de n observações para a variável X, é dada pelo quociente entre a soma dos valores observados e o número total de observações:

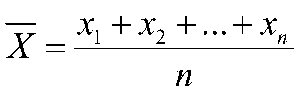
1.2) Média aritmética ponderada:

A média aritmética ponderada de um conjunto {x1, x2, ..., xk} de k observações para a variável X, com frequências absolutas é dada pela expressão:



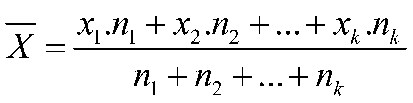
2) Moda:

É valor de maior frequência em uma série de dados, o que mais se repete.

Ex: Alguns alunos fizeram a segunda chamada de uma prova de matemática. Suas notas foram tabuladas na tabela abaixo:

3) Mediana:

Ordenando as observações de uma variável de forma crescente ou descrescente (Rol), a mediana é a observação que ocupa o valor central.

Ex.: A quantidade de atrasos dos alunos de uma turma, registrados por mês, de março a novembro, formam o seguinte conjunto de dados: 23, 34, 21, 48, 51, 20, 38, 29, 13.

Ordenando esses dados de forma crescente, temos:

13 – 20 – 21 – 23 – 29 – 34 – 38 – 48 – 51

Como há 9 observações, a observação central é a quinta:

13 – 20 – 21 – 23 – 29 – 34 – 38 – 48 – 51

Portanto, a mediana é igual a 29.

Cuidado! E se a quantidade de elementos da amostra não for um número ímpar? Se o tamanho da amostra for par, então não terá um elemento central. Dessa maneira, precisamos fazer a média aritmética simples entre os dois centrais.