Espelhos esféricos: método gráfico em Física

Classificação e elementos geométricos dos espelhos esféricos

Você já deve ter notado que, além dos sempre comuns espelhos planos, há também espelhos com outros formatos, como os esféricos. Estes estão presentes em situações em que se almeja produzir imagens aumentadas (espelhos côncavos) ou campos visuais maiores, necessários em determinados ambientes (espelhos convexos).

O desenhista e pintor holandês Mauritz Cornelis Escher (1898-1972) tem um trabalho fundamentado em xilografias, litografias e meios-tons que instiga a imaginação do observador. São figuras impressionantes, algumas verdadeiras distorções da realidade. Em sua obra reproduzida ao lado, o artista se autorretrata em seu escritório refletido em uma esfera espelhada — um espelho convexo — que permite uma visualização mais ampla do ambiente.

Considere a superfície esférica ∑ da figura a seguir, secionada por um plano π. O secionamento corta ∑ e determina uma “casca” esférica denominada calota.

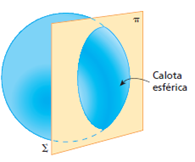
Se a superfície refletora da calota estiver voltada para dentro da esfera, o espelho esférico correspondente será denominado côncavo.

Representação de um espelho esférico côncavo.

Se a superfície refletora da calota estiver voltada para fora da esfera, o espelho esférico correspondente será denominado convexo.

Representação de um espelho esférico convexo.

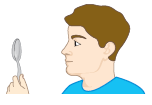
Uma colher de aço inoxidável tem comportamento semelhante ao dos espelhos esféricos. A face sobre a qual são colocados os alimentos é um espelho côncavo, enquanto a face oposta é um espelho convexo. É importante observar, entretanto, que essas colheres em geral não são superfícies esféricas.

Veja a seguir o esquema de um espelho esférico com seus principais elementos geométricos:

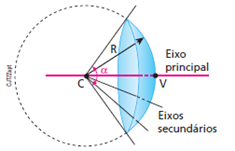
• O centro C da esfera que originou a calota é chamada de centro de curvatura do espelho.
• O polo V da calota é chamado de vértice do espelho .
• A reta que passa por C e V é chamada de eixo principal do espelho.
• Todas as demais retas que contêm o centro C são chamadas de eixos secundários.
• O ângulo α, que tem o vértice no centro C e os lados passando por pontos diametralmente opostos da calota, é chamdo de abertura do espelho.
• O raio R da esfera que originou a calota é denominado raio de curvatura do espelho.
• Qualquer plano perpendicular ao eixo principal é denominado plano frontal.

Espelhos esféricos gaussianos

Em geral, os espelhos esféricos não são sistemas ópticos estigmáticos, nem aplanéticos, nem ortoscópicos, como ocorre nos espelhos planos, uma vez que as imagens fornecidas por eles são sensivelmente distorcidas em comparação com os objetos correspondentes. As distorções provocadas por esses espelhos são denominadas aberrações de esfericidade.

Entretanto, o físico e matemático alemão Carl Friedrich Gauss (1777-1855) observou que, operando- se com raios luminosos pouco inclinados e pouco afastados em relação ao eixo principal (raios paraxiais), as aberrações de esfericidade inerentes aos espelhos esféricos ficavam sensivelmente minimizadas.

Neste capítulo, salvo recomendação em contrário, abordaremos os espelhos esféricos gaussianos, isto é, aqueles em que os raios luminosos envolvidos são pouco inclinados e pouco afastados em relação ao eixo principal. Por raios luminosos “pouco afastados” em relação ao eixo principal entendemos aqueles cuja distância do ponto de incidência ao referido eixo é pequena em comparação com o raio de curvatura do espelho. A representação esquemática dos espelhos esféricos gaussianos é a seguinte:

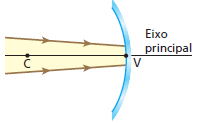
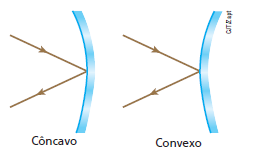Em relação ao pincel luminoso incidente representado na figura ao lado, o espelho esférico côncavo pode ser considerado gaussiano. Note que, nessas condições, o ângulo de abertura da região do espelho sobre a qual a luz incide não deve exceder 10°.

Focos dos espelhos esféricos

De maneira geral: O foco de um sistema óptico qualquer é um ponto que tem por conjugado um ponto impróprio (“situado no infinito”).

Ex.1:Radiotelescópios são equipamentos que rastreiam o espaço em busca de sinais — ondas eletromagnéticas compatíveis com as radiofrequências — provenientes dos mais remotos pontos do Universo. O elemento receptor desses dispositivos é uma superfície parabólica, cuja parte côncava tem alto poder de reflexão. Ondas planas incidem sobre o sistema, originando ondas esféricas refletidas que convergem para o foco do paraboloide, onde está instalado o elemento detector das informações.

Fotografia mostrando radiotelescópios

O fogão solar, projetado para ser utilizado no campo, funciona de maneira similar aos radiotelescópios. Raios solares paralelos incidem sobre um captador parabólico e, depois de refletidos, convergem para o foco do sistema, onde é colocada a panela contendo os alimentos.

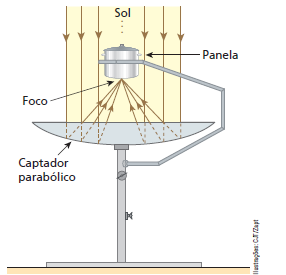Esquema de um fogão solar.

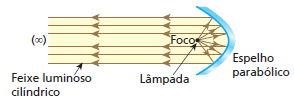
Ex.2: Nos colimadores, holofotes e refletores que emitem feixes luminosos cilíndricos (constituídos de raios paralelos), uma pequena lâmpada é instalada sobre o foco de um espelho parabólico côncavo que conjuga à fonte de luz uma imagem imprópria.

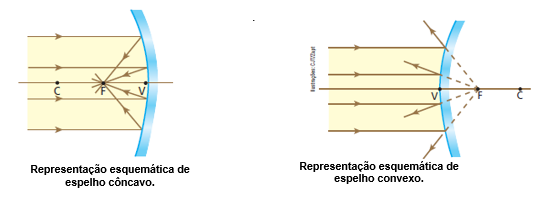
Considere os espelhos esféricos gaussianos a seguir, nos quais incidem raios luminosos paralelos entre si e ao eixo principal. A experiência mostra que as direções dos raios refletidos passam, necessariamente, por um mesmo ponto do eixo principal, denominado foco principal (F):

Suponhamos, agora, o caso em que incidem nos espelhos raios luminosos paralelos entre si e a um dos eixos secundários. Pode-se verificar, também nessa situação, que as direções dos raios refletidos passam por um mesmo ponto, mas do eixo secundário considerado. Esse ponto é denominado foco secundário (φ):

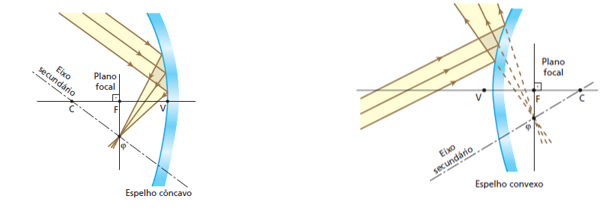
Prova-se, ainda, que o foco principal e os infinitos focos secundários de um espelho esférico gaussiano se alojam em um mesmo plano frontal, denominado plano focal.

É importantíssimo perceber que os focos de um espelho côncavo são reais, enquanto os de um espelho convexo são virtuais. A explicação para esse fato é simples: nos espelhos côncavos, os focos são determinados efetivamente pelos raios de luz (os focos apresentam-se “na frente” do espelho), enquanto nos espelhos convexos os focos são determinados pelos prolongamentos dos raios (os focos apresentam-se “atrás” do espelho). Observe agora o espelho esférico côncavo representado a seguir, no qual incide um raio luminoso paralelo ao eixo principal. Ao se refletir, o raio intercepta o eixo principal do espelho no ponto F (foco principal).

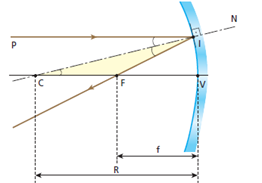
Na figura, temos:

CIP = FIC (2° lei da reflexão) CIP = ICF (alternados internos)

Portanto, FIC = ICF, e o triângulo FIC é isósceles, valendo a igualdade:

CF = FI

Mas FI = FV, pois o raio incidente considerado é paraxial. Assim:

CF = FV

Ou também:

F = R/2

A conclusão acima permite afirmar: Nos espelhos esféricos gaussianos, o foco principal é aproximadamente equidistante do centro de curvatura e do vértice.

Raios luminosos particulares

Nos espelhos esféricos, alguns raios luminosos particulares de simples traçado apresentam grande interesse, pois facilitam a construção gráfica das imagens.

1º raio particular

Todo raio luminoso que incide no espelho alinhado com o centro de curvatura se reflete sobre si mesmo.

Essa afirmação pode ser constatada de imediato, pois um raio luminoso que incide alinhado com o centro de curvatura é normal à superfície refletora. Como a incidência é normal, o ângulo de incidência é nulo, o mesmo devendo ocorrer com o ângulo de reflexão. Daí dizermos que “o raio se reflete sobre si mesmo”.

Usando a representação gaussiana, temos as figuras:

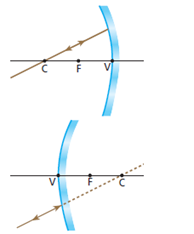
A propriedade que esse raio tem de refletir-se sobre si mesmo é verificada em qualquer tipo de espelho esférico, gaussiano ou não.

2º raio particular

Todo raio luminoso que incide no vértice do espelho gera, relativamente ao eixo principal, um raio refletido simétrico.

Essa afirmação é consequência da 2ª Lei da Reflexão. A reta normal à superfície refletora em V é o próprio eixo principal. Como o ângulo de reflexão deve ser igual ao de incidência, justifica-se a simetria citada.

Usando a representação gaussiana, temos as figuras:

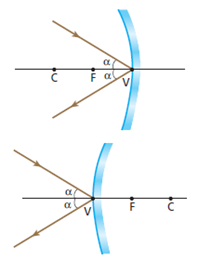
A propriedade que esse raio tem de refletir-se simetricamente em relação ao eixo principal é verificada com qualquer tipo de espelho esférico, gaussiano ou não.

3º raio particular

Todo raio luminoso que incide paralelamente ao eixo principal se reflete alinhado com o foco principal.

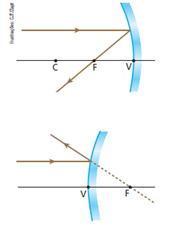
Note que essa afirmação decorre da própria definição de foco principal.

Considerando a reversibilidade dos raios de luz, podemos enunciar também:

Todo raio luminoso que incide alinhado com o foco principal se reflete paralelamente ao eixo principal.

Esse raio só é verificado em espelhos esféricos gaussianos.

Construção gráfica das imagens nos espelhos esféricos

Para construir a imagem de um ponto conjugada por um sistema óptico, necessitamos de pelo menos dois raios luminosos incidentes. Em relação ao traçado das imagens fornecidas pelos espelhos esféricos, devemos utilizar os raios luminosos particulares descritos na seção anterior.

Considere, por exemplo, o espelho convexo abaixo, diante do qual há um objeto AB que tem o extremo B no eixo principal. Nesse caso, para obter a imagem de AB, basta obtermos a imagem do extremo A, pois a imagem correspondente ao extremo B estará situada no eixo principal.

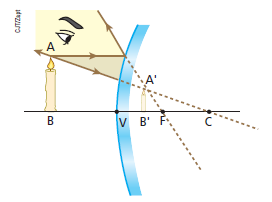
Observe que, nessa situação, a imagem formada é:

• Virtual: obtida pelo cruzamento dos prolongamentos dos raios refletidos (situada “atrás do espelho”);
• Direita: “de cabeça para cima” em relação ao objeto;
• Menor: o “tamanho” da imagem é menor que o do objeto.

É importante destacar que:

A um objeto real, um espelho esférico convexo conjuga uma imagem sempre virtual, direita e menor, compreendida entre o foco principal e o vértice, independentemente da distância do objeto à superfície refletora.

Aumentando ou dimuindo a distâcia entre a vela e a superfície refletora do espelho convexo, a imagem mantém suas características: virtual, direita e a menor que o objeto.

As características das imagens produzidas pelos espelhos côncavos, por sua vez, dependem da posição do objeto em relação ao espelho. Há cinco casos importantes a considerar:

1º Objeto além do centro de curvatura

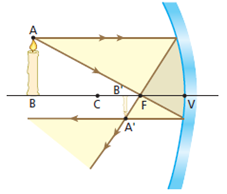
Características da imagem:

• Real: formada pelo cruzamento efetivo dos raios refletidos;
• Invertida: “de cabeça para baixo” em relação ao objeto;
• Menor: o “tamanho” da imagem é menor que o do objeto

Na fotografia, imagem real, inevrtida e menor produzida por um espelho esférico côncavo de um objeto situado além do seu centro de curvatura.

2º Objeto no plano frontal, que contém o centro de curvatura

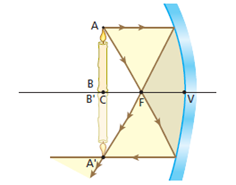
Características da imagem:

• Real;
• Invertida;
• Do mesmo tamanho que o objeto.

3º Objeto entre o centro de curvatura e o foco

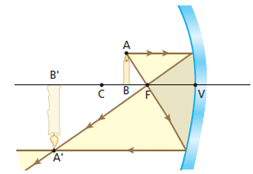
Características da imagem:

• Real;
• Invertida;
• Maior: o “tamanho” da imagem é maior que o do objeto.

Obs.: Observe que as imagens reais obtidas de objetos também reais são sempre invertidas.

4º Objeto no plano focal

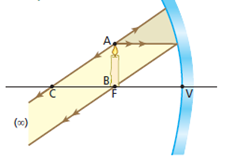
Nesse caso, como os raios luminosos emergentes do sistema são paralelos entre si, a imagem “forma-se no infinito”[1], sendo, portanto, imprópria.

5º Objeto entre o foco e o vértice

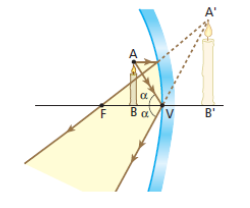
Características da imagem:

• Virtual;
• Direita;
• Maior.

Esse é o único caso em que, de um objeto real, o espelho côncavo conjuga imagem virtual.[2]

Obs.: É muito comum se ouvir falar dos pares: imagem real é sempre invertida e imagem virtual é sempre direita! Cuidado! Isso só vale para sistemas óticos simples, isto é, um espelho ou uma lente