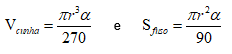Definição de Esfera
Seção Plana numa Esfera
Volume da Esfera
Área da Esfera
Cunha e Fuso da Esfera
Esferas
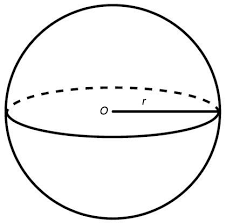
Esfera é um sólido limitado por uma superfície esférica fechada e que tem todos os seus pontos à mesma distância de um ponto em seu interior.
Área da superfície esférica
Seja uma esfera de centro O e raio R. A área da superfície esférica é dada pela fórmula:
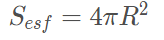
Volume de uma esfera
Como Arquimedes deduziu a fórmula da esfera?
Arquimedes pegou um cilindro de raio r e encheu-o de líquido. Colocou um recipiente por baixo do cilindro e, em seguida colocou dentro do cilindro uma esfera de raio r. Ao fazê-lo o líquido que estava dentro do cilindro transbordou para o recipiente. Deitou fora o líquido que sobrou (dentro do cilindro) e colocou o líquido do recipiente novamente dentro do cilindro verificou assim que o líquido da esfera ocupava 2/3 do cilindro:
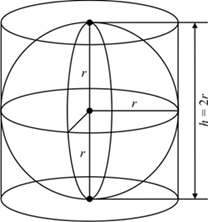
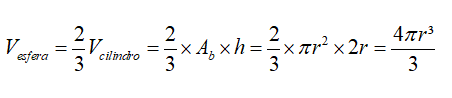
Logo,
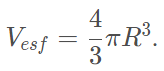
Secção em uma esfera
Toda seção plana de uma esfera é um círculo. Sendo R o raio da esfera, d a distância do plano secante ao centro e r o raio da seção, observe:
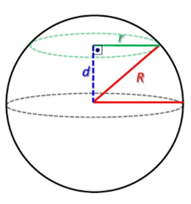
Assim, pelo triângulo pitagórico, temos que R² = d² + r².
Calota esférica
Se cortarmos a esfera por um plano que não contém seu centro, as superfícies formadas se chamarão de calotas esféricas.
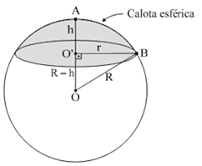
- A área da calota esférica é dada pela fórmula
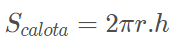
- O volume da calota esférica é dado pela fórmula
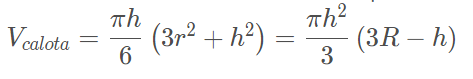
Fuso e cunha esférica
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semicircunferência de um ângulo α em torno de seu eixo:
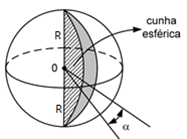
Já a cunha esférica é a parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo α. A área e o volume do fuso esférico e da cunha esférica, respectivamente, podem ser obtidos por uma regra de três simples:
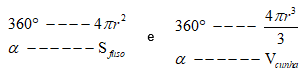
Assim, chegamos nas fórmulas: