Definição
Acompanhe a aula sobre Escalonamento
Regras para o escalonamento
Sistema três por três
Casos Especiais
Método de escalonamento
Um sistema linear é dito escalonado se a última linha tiver apenas uma incógnita, a penúltima duas, e assim sucessivamente até a primeira linha onde terão todas as incógnitas. Segue exemplo de um sistema escalonado:
annxn = bn
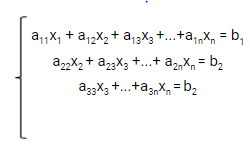
Procedimentos para escalonar um sistema
- Fixamos como 1ª equação uma das que possuam o coeficiente da 1ª incógnita diferente de zero.
- Utilizando as propriedades de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das demais equações.
- Anulamos todos os coeficientes da 2ª incógnita a partir da 3ª equação
- Repetimos o processo com as demais incógnitas, até que o sistema se torne escalonado.
Exemplo:
Dado o sistema linear:
x + 2y + 4z = 0
2x + 3y - z = 0
- x + 16z = 4
Vamos resolver o sistema pelo método de escalonamento.
x + 2y + 4z = 0 * (-3)
2x + 3y - z = 0 * (2)
-x + 16z = 4
-3x – 6y – 12z = 0
4x + 6y – 2z = 0
x – 14z = 0
Substitua na segunda equação:
x + 2y + 4z = 0
x - 14z = 0
- x + 16z = 4
Soma a segunda equação com a terceira:
x + 2y + 4z = 0
x - 14z = 0
2z = 4