Equilíbrio, momento e centro de massa em Física

Equilíbrio do corpo extenso

Tratar um corpo como um ponto material equivale a admitir que, na situação em que está sendo estudado, só interessa considerar a possibilidade de ele adquirir algum movimento de translação, já que não se pode caracterizar o movimento de rotação de um corpo puntiforme. Por isso, dizemos que o equilíbrio de um ponto material é de translação.

O corpo extenso, por sua vez, pode apresentar tanto o movimento de translação como o de rotação. Por esse motivo, o estudo do equilíbrio do corpo extenso requer duas análises: um referente à translação e outro referente à rotação.

Para um corpo extenso estar em equilíbrio, é necessário satisfazer duas condições: um referente ao equilíbrio de translação e outra ao equilíbrio de rotação.

Condição de equilíbrio de translação

A condição de equilíbrio de translação de um corpo extenso (centro de massa em repouso ou em movimento retilíneo e uniforme) é que a resultante das forças externas atuantes no corpo seja nula:

F_ext = 0 

Condição de equilíbrio de rotação

A condição de equilíbrio de rotação de um corpo extensivo sob a ação de um corpo extenso sob a ação de um sistema de forças coplanares é que a soma algébrica dos momentos escalares de todas as forças em relação a qualquer eixo perpendicular ao plano das forças seja nula:

ΣM = 0 

A condição de equilíbrio de rotação pode ser expressa de outra maneira. Considerando todos os momentos em módulo, podemos escrever que a soma de todos os momentos horários (M_H) é igual à soma de todos os momentos anti-horários (M_AH):

M_H = M_AH

Que parada é essa de “momento de uma força”?

Momento de uma força (M₀) em relação a um eixo

Procuraremos aqui uma grandeza capaz de medir a eficiência de uma força em produzir rotação em um corpo. Para isso, vamos considerar uma situação prática.

Situação: A gangorra é um sistema que permite investigar a eficiência de uma força em produzir rotação:

Na gangorra da Figura 1, temos dois meninos (A e B) sentados em pontos diferentes da gangorra. Nota que a gangorra não está rotacionando. Isso significa que ela está em um equilíbrio de rotação. Sendo o peso do garoto A é o dobro do peso do garoto B, é necessário que a distância de B até o eixo E seja o dobro da distância de A até esse mesmo eixo para que ambos fiquem em equilíbrio.

Agora, podemos montar uma definição a partir do observado

Definição

Podemos concluir que a eficiência de uma força em produzir rotação em um corpo é tanto maior quanto maiores forem sua intensidade e a distância entre a reta que passa pela força – denominada linha de ação – e o eixo de rotação do corpo. A grandeza física que mede essa eficiência é denominada momento ou torque.

Para definir de forma escalar essa grandeza, considere um corpo sob a ação da força F e um eixo de rotação (real ou imaginário) perpendicular ao plano da figura e passando pelo ponto O (polo do momento/ponto de apoio/fulcro/ponto de giro/ponto de rotação/eixo de rotação). A força F e o ponto O estão no plano do papel. A distância d, de O até a linha de ação de F, denomina -se braço de F em relação a O. Assim, definimos:

O módulo do momento escalar ou torque (M) da força F em relação a O é o produto da intensidade dessa força pelo seu braço em relação a O, precedido de um sinal algébrico arbitrário:

M = F . d 

Unidade (SI): [M] = N.m

Mas... A situação da gangorra desconsiderou o peso da própria gangorra. Seria possível o próprio peso da gangorra gerar uma rotação? Claro!

Momento de uma força feito pela propria barra

Se a situação analisada não desconsiderar o Peso ou a massa da barra, então temos mais uma Força para gerar Momento além das forças sendo feitas na barra. Mas onde vamos marcar esse Peso da barra? Afinal, é preciso de uma força e uma distância para se calcular o Momento. Bom... A Força Peso da barra será marcada no centro de massa da barra.

Centro de massa (CM): ponto em que se pode admitir que a massa está concentrada. Para uma figura homogênea, esse ponto é o centro geométrico do corpo.

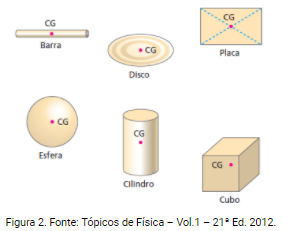
Por exemplo, o centro de massa de um quadrado é no encontro de suas diagonais, do círculo é no seu centro e no triângulo é no baricentro. O centro de massa pode ser calculado para uma figura linear, plana ou volumétrica.

Observe o centro de massa de algumas geometrias regulares.