Equações e Inequações de 1º e 2º Grau em Matemática

O que é uma equação?

Chamamos de equação a sentença matemática uma expressão algébrica que contém uma igualdade. Pode possuir uma ou mais incógnitas. Por exemplo: 3x − 3 = 3

Uma característica fundamental da equação é que o 1° membro (à esquerda do sinal de igual) é igual o 2° membro (à direita do sinal de igual).

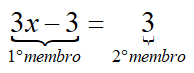
Resolver uma equação implica em descobrir qual o valor do x que satisfaz essa sentença.

Uma regra importante é que dada a equação, é possível realizar qualquer operação numérica, desde que a operação feita ao 1° membro seja a mesma feita no segundo membro. No nosso exemplo, podemos somar 3 a ambos os membros:

3x − 3 = 3
3x − 3 + 3 = 3 + 3
3x = 6

Equação do 1° grau

Definimos como equação do primeiro grau, aquela que pode ser escrita da forma ax + b = 0, onde a e b são números quaisquer. Note que se subtrairmos 3 em ambos os lados da equação temos:

3x − 3 = 3
3x − 3 + 3 = 3 + 3
3x = 6
3x − 6 = 0

Outra caracterização da equação do 1° grau é que o maior expoente do x nesse caso é 1 (lembrando que elevar a 1 não muda valores). Dessa forma, é razoável pensar que existam equações de outros graus como 2, 3 e por aí vai.

Raízes da uma equação

São valores possíveis que satisfazem a equação. Em outras palavras, descobrir a raiz da equação é descobrir quanto vale o x. No exemplo anterior:

3x = 6

x = 2

Logo x = 2 é o valor que faz a equação ser verdadeira.

3x − 3 = 3
3.(2) − 3 = 3
6 − 3 = 3
3 = 3

Vale ressaltar que qualquer outro valor colocado no lugar de x, torna a igualdade falsa.
Se usarmos x = 5, chegaremos que 9 é igual a 3 o que é falso.

3x − 3 = 3
3.(5) − 3 = 3
15 − 3 = 3
9 = 3

Resolução de uma equação

De forma geral, para resolver uma equação:

• Deixar “números” de um lado e “letras” do outro;
• Juntar termos semelhantes usando as operações matemáticas
• Encontrar o valor da incógnita

Equação do segundo grau

Definição

É toda equação que pode ser reduzida à forma:

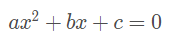
Com a,b,c ∈ R e a ≠ 0. a,b,c são chamados de coeficientes.

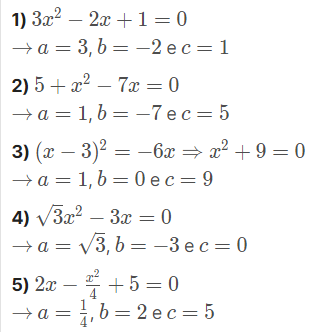
Obs: Os exemplos 1, 2 e 5 são chamados de equações completas pois possuem todos os coeficientes, já os os exemplos 3 e 4 são chamados de equações incompletas pois não possuem todos os coeficientes.

Equação incompleta: b = 0

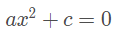
Exemplos:

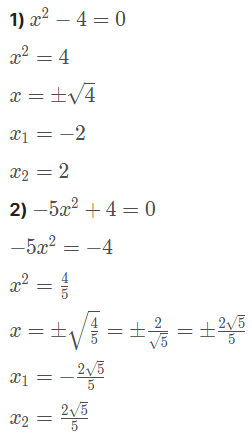
Equação incompleta: c = 0

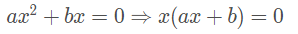
Exemplos:

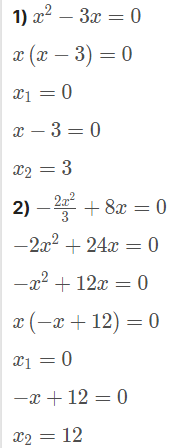
Equação completa: fórmula de Bhaskara

Quando a equação do segundo grau é completa, para encontrar as raízes, deve-se usar a fórmula de Bhaskara.

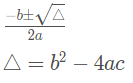
Obs: Delta (△) é chamado de discriminante.

Exemplos:

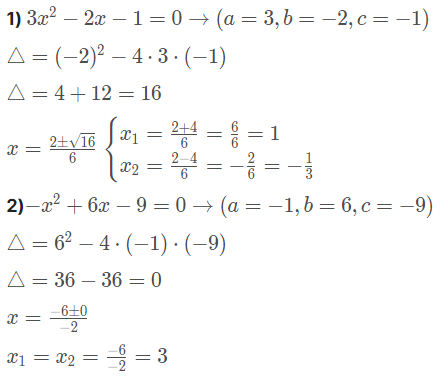
Discussão das Raízes

Relações entre coeficientes e raízes

É possível encontrar as raízes de uma equação do segundo grau através de relações entre os coeficientes. Chamamos este método de “soma e produto”. Observe:

Soma das raízes

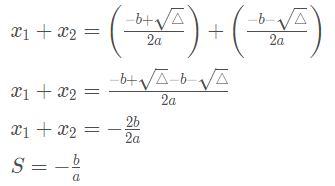
Produto das raízes

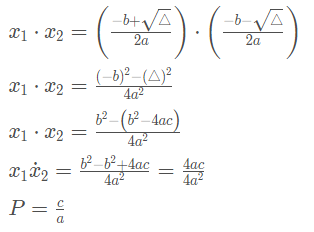
Portanto as raízes de uma equação serão os dois números que somados resultarão em -b/a e multiplicados resultarão em c/a.