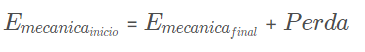Teorema trabalho energia cinética
Energia Potencial
Exemplo sobre conservação de energia mecânica
Exemplo de conservação de energia em um plano inclinado
Exemplo de conservação de energia e força centrípeta
Exemplo de arremesso de uma catapulta
Exemplo de energia mecânica não conservada
Em Cinemática, aprendemos que um corpo pode descrever diversos tipos de movimento e esse movimento tinha como base uma analise de forças. Agora, vamos utilizar outro parametro. Na aula de Energia mecânica vamos analisar o movimento de um corpo atraves da Energia mecânica que esse corpo apresenta. Energia e Trabalho são grandezas de mesma dimensão, logo, vamos utilizar a unidade “Joule” para representa-las no SI (isso significa que vamos trabalhar no SI com todas as grandezas que vão aparecer aqui!).
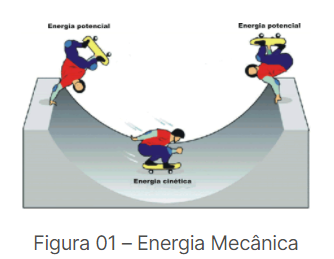
A energia mecânica de um corpo é a soma de três tipos de energias: A energia cinética, energia potencial elástrica e energia potencial gravitacional.
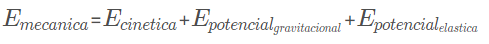
Energia Potencial Gravitacional
Um corpo apresenta energia potencial gravitacional quando ele esta posicionado em um ponto que apresenta um desnível em relação ao referêncial adotado. Logo, viu que o corpo tem uma altura, ele tem energia potencial gravitacional.
Energia Potencial Elástica
Um corpo apresenta energia potencial elástica quando esse corpo esta deformando uma determinada mola no ponto onde ele esta posicionado. Logo, viu mola sendo puxada ou comprimida, tem energia potencial elástica.
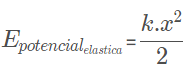
Energia Cinética
Um corpo apresenta energia cinética quando esse corpo desenvolve algum tipo de movimento. Por conta disso, esse corpo tem uma velocidade. Logo, viu que o corpo tem velocidade, esse corpo tem energia cinética.
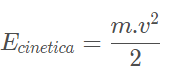
Teorema da Energia Cinética
Lembra que no inicio desse resumo falamos que Energia e Trabalho são grandezas de mesma dimensão e que usamos a mesma unidade? Não foi a toa! Por apresentarem essa semelhança, temos uma expressão matemática que liga essas duas grandezas. Essa forma recebe o nome de Teorema da Energia Cinética.
Considere uma força constante F que atua sobre um corpo de massa m, na direção e no sentido do movimento e sendo F a sua força resultante. O trabalho realizado é:
W = F.∆S = m.a.∆S
Podemos utilizar a equação acima e juntar com Torricelli da seguinte forma:
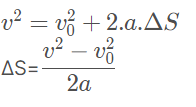Escrevendo substituindo o ∆S da equação de trabalho pelo ∆S que encontramos em Torricelli, temos:
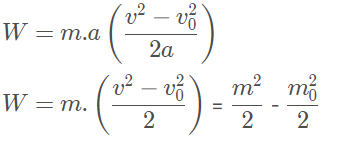W = ∆Ecinética
Claro, você não precisa decorar o desenvolvimento, só o resultado final dele. A ideia de ter esse desenvolvimento no resumo é para mostrar de onde veio essa expressão.
Conservação de Energia
Aqui vem o grande objetivo de aprendemos Energia Mecânica. A conservação da energia mecânica só acontece em sistemas que não apresentam forças dissipativas, ou seja, precisamos de uma situação sem atrito e sem resistência do ar.
O Princípio da Conservação da Energia diz que ao calcular a Energia Mecânica de um corpo em um determinado ponto (vamos chamar esse ponto de ponto inicial), essa energa mecânica vai aparesentar um valor que será o mesmo para qualquer outro ponto escolhido dentro do sistema. A energia poderá sofrer mudanças na sua classificação, ou seja, você pode calcular um ponto que só tenha energia cinética o outro ponto só tem potencial gravitacinal, mas continuará sendo expressa pelo mesmo número.
Quando aplicamos o Princípio da Conservação de Energia em sistemas mecânicos, estamos dizendo que a energia mecânica será mecânica até o fim do processo, isto é, não será transformada em outra forma de energia.
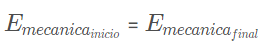
Sistemas não conservativos
Caso o seu sistema apresente uma força dissipativa, vamos entender que teremos perda de energia mecânica. Entenda que “perda de energia mecânica” quer dizer que a energia mecânica desse corpo será transformada em qualquer outro tipo de energia que não esta ligada ao movimento dele. Caso você depare com algum sistema desses, você pode pensar que, de um ponto a outro, a energia mecânica no inicio é igual a energia mecânica no final mais a perda.
