Dinâmica em Física

A dinâmica é a parte da Física relacionada à mecânica que estuda os movimentos e as causas que os produzem e os modificam. Existem três Leis que regem na Dinâmica, mas antes de apresentá-las vamos introduzir o conceito de força. O primeiro ponto a ser falado é que força é uma grandeza vetorial, ou seja, tem módulo, direção e sentido. E sua finalidade é alterar o estado de repouso ou movimento de um corpo ou deformá-lo. E divide-se a força em duas características básicas, que são elas:

• 
  Campo: São as forças que atuam sem um contato direto como resultado da existência de um campo – um região do espaço onde efeitos físicos específicos se fazem sentir, como por exemplo temos a força magnética, força elétrica e força gravitacional.
• Contato: São as forças em que ocorre um contato direto entre as superfícies dos corpos que estão interagindo, como por exemplo a força normal, força de tração, força elástica e a força de atrito.

Marcando as Forças

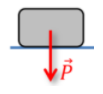
• Peso

Força de interação entre qualquer corpo de massa m com um campo gravitacional e pode ser calculado com a equação:

P = m.g

Onde g é a aceleração da gravidade local. Note que, como a massa é sempre maior do que zero, P tem sempre a mesma direção e sentido de g.

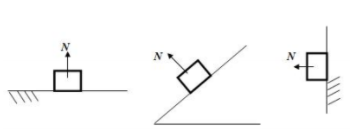
• Normal

Força de interação de um corpo e uma superfície. A força normal será sempre perpendicular à superfície e no sentido da superfície para o corpo.

Não existe uma equação específica para calcular a força normal, deverá ser feito uma análise das forças aplicadas na direção da normal e, por um sistema linear, determinar seu valor.

Atenção: Normal não forma par ação e reação com o Peso!!!

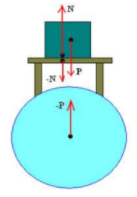
• Tração

Força que aparece sempre em cabos, fios e cordas quando esticados. Cada pedaço da corda sofre uma tração, que pode ser representada por um par de forças iguais e contrárias que atuam no sentido do alongamento da corda. Dinamômetro: disposto que pode ser acoplado à corda para medir a intensidade da força de tração.

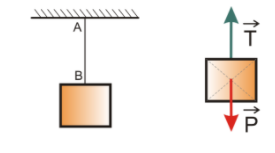
• Força Elástica

Força que aparece durante a deformação de algum corpo com características elásticas, ou seja, que pode ser deformado durante a aplicação de uma força e que tem a capacidade de voltar ao seu tamanho original assim que a força for cessada. Corda de borracha, elásticos e molas são os exemplos mais comuns em questões.

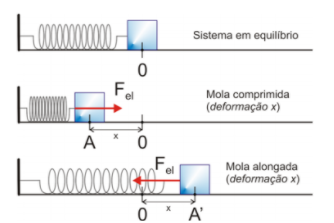
A força elástica é um vetor que tem mesma direção e sentido oposto à força aplicada para deformar a mola em questão, sendo assim chamada de força de restituição. O módulo da força elástica pode ser calculado pela equação:

F = -kx

Onde k é o coeficiente de elasticidade (característica da mola) e x é a deformação sofrida pela mola.

• Força de atrito

Para introduzirmos ao assunto, vamos considerar que você está empurrando uma geladeira sobre uma superfície irregular. Admitindo que essa geladeira esteja, inicialmente, em repouso. Quando você exerce sobre a geladeira uma força horizontal (F), surge uma força que opõe à tendência de movimento. Enquanto a geladeira não se mover, essa força que se opõe à tendência de movimento, denominada atrito estático, possui intensidade igual à da força que está solicitando o movimento, no caso, a força horizontal (F) exercida por você.

Verifica-se que, se a intensidade da força exercida por você for aumentada, haverá um momento em que a geladeira atingirá a situação de iminência de movimento. Nesse instante, a força de atrito (Fat), que continua tendo a mesma intensidade que a força exercida pelo homem, atinge seu valor máximo, denominado atrito estático máximo.

A partir do momento em que você aumentar um pouco mais a força aplicada à geladeira, esta vai entrar em movimento, e o atrito no bloco será dito dinâmico (ou cinético).

Atrito Dinâmico ou Cinético

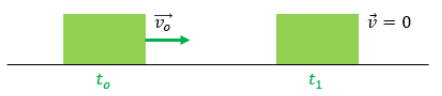
Quando um corpo é lançado com velocidade inicial vo numa mesa, ou como o exemplo descrito anteriormente, ele adquire um movimento retardado até parar. A força que garante a sua desaceleração é chamada força de atrito dinâmico ou cinético e é uma projeção da força de contato entre a mesa e o bloco.

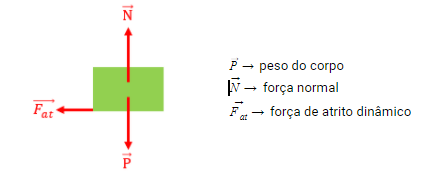
Representando as forças que atuam no bloco, num instante qualquer do seu movimento, temos:

A força F aplicada sobre o bloco é dada por:

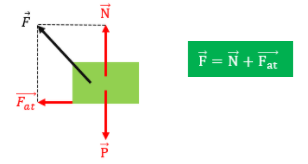
Experimentalmente, verificamos que o módulo da força de atrito cinético é praticamente constante e proporcional ao valor da componente normal (N) que o corpo exerce na superfície.

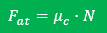
O coeficiente de proporcionalidade c é chamado coeficiente  de atrito cinético. É uma grandeza adimencional e depende do material de que é feito cada corpo e o grau de polimento das superfícies em contato.

Atrito Estático

Se um corpo estiver em repouso sobre uma superfície horizontal, a força de contato é normal à superfície, como vocês já viram anteriormente, e sobre ele é aplicado uma força, e momentos antecendentes a ele começar seu movimento, teremos a seguinte situação:

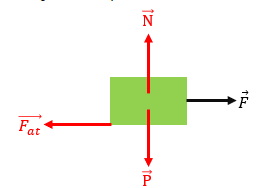
Nesse momento, conforme já dito no início desse conteúdo, a força de atrito (Fat) é igual à força (F). Mas, se numa mesma situação em que o bloco estiver sobre um plano inclinado, teremos:

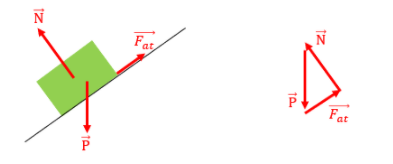
Se aumentarmos gradativamento o ângulo de inclinação do bloco, com o bloco ainda em repouso, aumentará também a intensidade da força de atrito estático. Para um valor máximo de θ, o bloco fica na eminência de descer o plano. Neste instante, atua a força de atrito estático máximo. Seu valor, em módulo, é dado por:

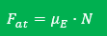
Relação entre o coeficiente de atrito estático e dinâmico (cinético)

Experimentalmente é simples constatar que é mais fácil manter um corpo em movimento retilíneo uniforme, escorregando sobre uma superfície, do que fazer o mesmo corpo, sobre a mesma superfície, entrar em movimento acelerado ou retardado. Logo, podemos escrever:

Para um mesmo par de superfícies em contato, o coeficiente de atrito cinético é menor que o coeficiente de atrito estático.

Leis de Newton

• Princípio da Inércia (1ª Lei de Newton)

É definido como:

Se a força resultante sobre uma partícula é nula, ela permanece em repouso ou em movimento retil[ineo e uniforme, por inércia.

Note que, para variar a velocidade vetorial de um corpo, é necessária a intervenção de uma força resultante, fruto das ações de agentes externos ao corpo. Sozinho (livre de força resultante externa), um corpo em movimento mantém velocidade constante, por inércia.

• Princípio Fundamental da Dinâmica (2ª Lei de Newton)

Consideremos uma partícula submetida à ação de uma força resultante F. O que devemos esperar que aconteça com essa partícula? Ela adquirirá uma aceleração a, isto é, experimentará variações de velocidade com o decorrer do tempo. Supondo que F seja horizontal e dirigida para a direita, qual será a direção e o sentido de a? Mostra a experiência que a terá a mesma orientação de F, ou seja, será horizontal para a direita.

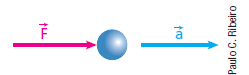
Ou, de forma genérica:

F = m a

Escrevendo essa expressão na forma vetorial, temos:

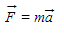
Força [F] = kg.m/s² = kg.m.s-2 = N (newton).

• 3ª Lei de Newton

Um experimento simples que você já deve ter realizado está esquematizado na figura abaixo, na qual está representado um balão de borracha movimentando-se à medida que expele o ar existente em seu interior.

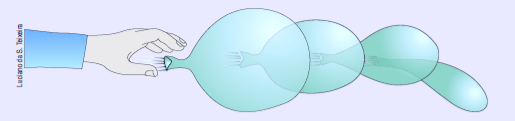
Esse fenômeno pode ser explicado pelo Princípio da Ação e da Reação. Cada partícula do ar ejetado recebe “força para trás”. Essas partículas, que são em grande número, reagem no balão com “pequenas forças para a frente”. Essas “forças” originam uma força resultante expressiva, capaz de acelerar o corpo elástico.

Toda ação acompanha uma reação com forças de:

• Mesmo módulo;
• Mesma direção;
• Sentidos opostos;
• Atuam em corpos diferentes.

Força Centrípeta

Na figura seguinte, representamos uma partícula de massa m, vista num instante em que sua velocidade vetorial é  v.

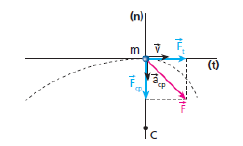
A trajetória descrita por ela é uma curva que, para a posição destacada no esquema, tem raio de curvatura R. Seja, ainda, acp a aceleração centrípeta comunicada por Fcp. Aplicando a 2ª Lei de Newton, podemos escrever que:

F_cp=m. a_cp

Conforme vimos em Cinemática Vetorial, o módulo de acp é dado pelo quociente do quadrado do módulo de v por R, isto é:

a_cp = v² / R

Assim, a intensidade da componente centrípeta da força resultante fica determinada por:

F_cp = m.v² / R