Determinantes e Sistemas lineares em Offline

Determinantes: Ordem 2 e ordem 3

Determinante é um número associado a uma matriz quadrada que tem inúmeras aplicações na Matemática, dentre as quais podemos destacar as operações entre vetores na Álgebra Linear e o Teorema de Cramer para a resolução de sistemas lineares. Vamos aprender a calcular determinantes!

Matriz quadrada de ordem 1: é o valor único da matriz.

A = [a​₁₁​​] → det A = a_11​​

Matriz quadrada de ordem 2: é a diferença entre o produto dos termos das diagonais principal e secundária.

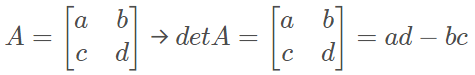
Exemplo:

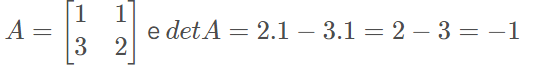
Matriz quadrada de ordem 3: usamos a regra de Sarrus.

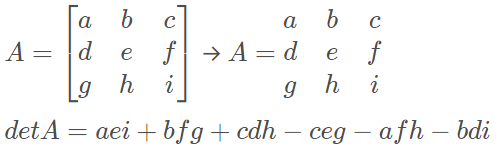
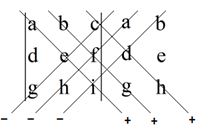
 Exemplo:

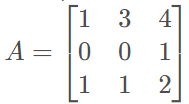
Pela regra de Sarrus , duplicamos as duas primeiras colunas e fazer a conta:

detA = (1∙0∙2) + (3∙1∙1) + (4∙0∙1) - (4∙0∙1) - (1∙1∙1) - (3∙0∙2) = 0 + 3 + 0 - 0 - 1 - 0 = 2

Sistemas Lineares

Existem diversas métodos para solucionar sistemas lineares, mas os mais usados são o método da substituição e o método da soma. 

Método da substituição

Solução de sistemas pelo método da substituição.

• Passo 1: Escolher uma incógnita e calcular seu valor algébrico.
• Passo 2: Substituir o valor algébrico da incógnita na outra equação.
• Passo 3: Calcular o valor numérico de uma das incógnitas.
• Passo 4: Substituir o valor numérico de x em qualquer uma das duas equações e encontrar o valor numérico de y.

Exemplo: Encontre a solução do sistema a seguir:

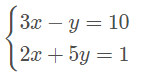
Escolhi a incógnita y na 1ª equação:

3x – y = 10
-y =10 - 3x
y = 3x - 10

Substituindo na segunda equação esse valor algébrico de y.

2x + 5y = 1
2x + 5* (3x- 10) = 1
2x + 15x – 50 = 1
17x = 51
x = 3

Após encontrar o valor numérico de x, escolha uma das equações para cumprir o quarto e último passo: obter o valor numérico de y. Escolhemos, para isso, a primeira equação. Observe:

2x + 5y = 1
2 * 3 + 5y = 1
5y = 1 – 6
5y = -5
y = -1

A solução desse sistema é S = {3, -1}.

Método da adição

Este método é bem eficaz em sistemas lineares 2x2:

• Passo 1: Escolher uma incógnita e multiplique sua equação pelo valor numérico da mesma incógnita em outra equação.
• Passo 2: Faça o mesmo na outra equação escolhida, mas agora multiplicando pelo valor numérico da incógnita da primeira equação.
• Passo 3: Soma essas duas equações.
• Passo 4: Após encontrar o valor de uma incógnita, volte em qualquer uma das duas equações originais e substitua o valor encontrado para encontrar o valor da outra incógnita

Exemplo:

Resolva o sistema linear a seguir pelo método da adição.

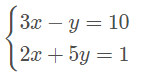
Escolhi a incógnita y, então, vou multiplicar uma pela outra.

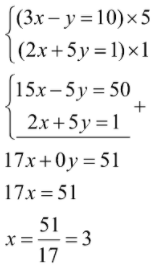
Volto para qualquer uma das equações originais e substituo o valor de x = 3.

3x - y = 10
3 * 3 – y = 10

y = 10 – 9
y = -1

S = {3, -1}