Como se faz uma decomposição
Porque se deve decompor forças
Decomposição do Peso em plano inclinado
Exercício de blocos em plano inclinado
Exercício de plano inclinado com atrito
Decomposição de forças em situação de equilíbrio
Plano Inclinado
Toda grandeza vetorial pode ser decomposta em componentes ortogonais X e Y.
Exemplo: Seja F uma grandeza vetorial que faz um certo ângulo com a direção horizontal de acordo com a figura abaixo. A grandeza vetorial F possui uma projeção ortogonal sobre o eixo X e outra sobre o eixo Y, as quais são descritas pelas expressões ao lado direito da figura abaixo.
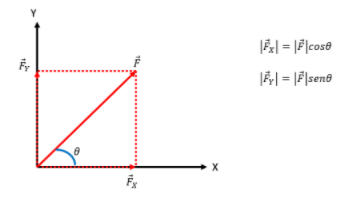
Para fazer a decomposição, utilizaremos sempre o triângulo:
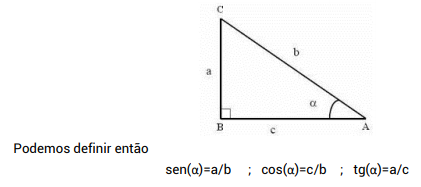
Considere um bloco deslizando num plano inclinado, sem atrito, que forma um ângulo θ com a horizontal. Note que, ao marcar o peso e a normal, elas não podem se equilíbram, pois não tem a mesma direção. Usamos um referencial XY inclinado em relação à horizontal e com o X na direção do movimento e fazemos a decomposição da força peso nas componentes X e Y do novo referencial.
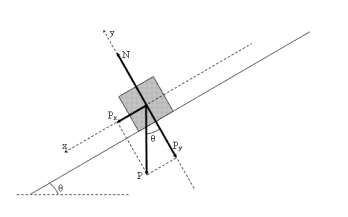
Como não existe movimento na direção Y do referencial, podemos afirmar que a normal equilibra a componente Y do peso. Note também que no eixo X haverá uma força resultante que atua no bloco, a componente X do peso.
Podemos escrever então:
N = Py = P.cosα
FR = Px = P.sinα
Importante: O ângulo entre o plano inclinado e a horizontal é igual ao ângulo entre a vertical e a reta perpendicular ao planto inclinado. De acordo com o desenho acima, o ângulo θ formado entre o plano inclinado com a horizontal é o mesmo que o eixo X forma com a força peso.