Circunferência em Matemática

Circunferência

Definição

Circunferência é o nome dado ao conjunto de pontos do plano equidistantes de um ponto fixo, que chamamos de centro.

Equação reduzida

Uma circunferência y de centro no ponto C(Xo, Yo) e raio de medida R é o conjunto dos pontos P(X, Y) tais que P pertence a y e PC = R

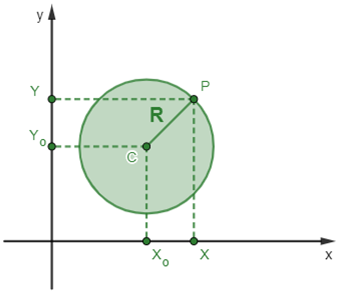
Substituindo PC por seu valor, de acordo com a fórmula da distância entre dois pontos tem-se:

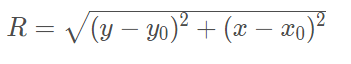
Ao elevar ambos os lados ao quadrado, chegamos à equação da circunferência:

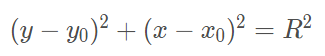
Obs.: Repare que, se o centro da circunferência for em (0, 0), teremos a equação R² = x² + y²

Ex: Vamos obter a equação reduzida da circunferência de centro C(1, 2) e raio igual a 5.

Equação geral

A equação geral da circunferência é obtida a partir da equação reduzida, para isso, iremos resolver o produto notável e igualar a equação à zero. Observe:

Ex: Vamos descobrir a equação geral da circunferência abaixo:

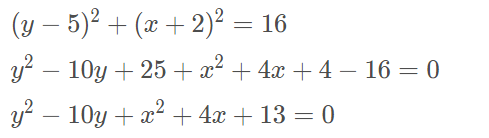
Transformando a equação geral na reduzida

Uma dos processos mais importantes é saber transformar uma equação geral na equação reduzida.

Vamos aprender a partir de um exemplo:

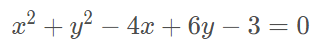
O primeiro passo é juntar os termos que tiverem y e os termos que tiverem x .

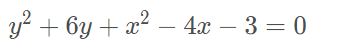
Agora iremos manipular a equação inserindo termos que não alterem a igualdade.

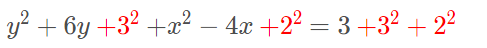
Já temos o quadrado perfeito que podemos juntar:

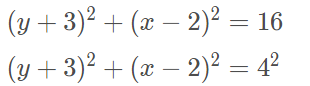
Pronto, encontramos a equação reduzida dessa circunferência e agora podemos dizer que as coordenadas do centro são C(2,−3) e o raio R = 4.

Posições relativas

Vamos agora comparar alguns elementos com a circunferência.

Ponto x Circunferência

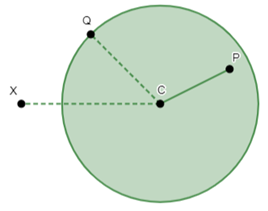
• Quando a distância entre um ponto e centro da circunferência for menor que o raio, dizemos que esse ponto é interno à circunferência (ponto P).
• Quando a distância entre um ponto e o centro da circunferência for igual ao raio, dizemos que esse ponto está inscrito na circunferência (ponto Q).
• Quando a distância entre um ponto e o centro da circunferência for maior que o raio, dizemos que esse ponto é externo à circunferência (ponto X).

Reta x Circunferência

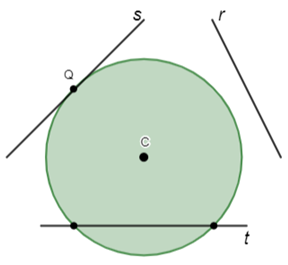
• Quando a reta não tem nenhum ponto comum com a circunferência, dizemos que a reta é externa à circunferência (reta r).
• Quando a reta tem apenas um ponto em comum com a circunferência, dizemos que a reta é tangente à circunferência (reta s).
• Quando a reta cruza a circunferência em dois pontos, dizemos que essa reta é secante à circunferência. (reta t)

Circunferência x Circunferência

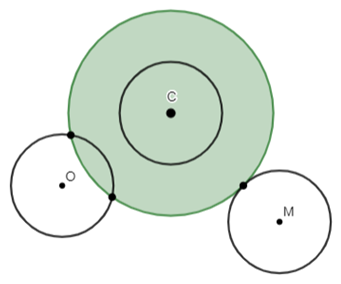
• Se uma circunferência tiver o mesmo centro que outra, dizemos que elas são concêntricas.
• Se uma circunferência tangencia outra circunferência dizemos que ela tangencia a outra.
• Se uma circunferência cruza outra em dois pontos, dizemos que ela é secante à outra.