Definição
Arcos côngruos
Linhas trigonométricas: seno e cosseno
Linhas trigonométricas: tangente e secante
Linhas trigonométricas: cotangente e cossecante
Resumão
Ciclo trigonométrico
Considere uma circunferência de raio = 1 e centro (0,0). Essa circunferência é chamada de ciclo trigonométrico.
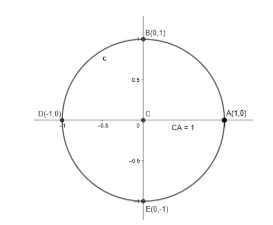
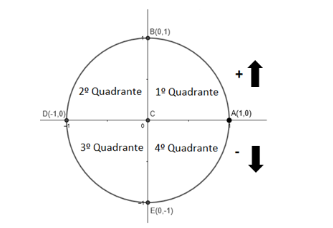
- Convencionou-se como sentido positivo dos arcos o sentido anti-horário.
- Os eixos coordenados dividem o ciclo trigonométrico em 4 quadrantes:
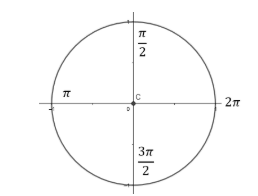
Cada número real x (0 < x < 2) está associado a um ponto x da circunferência, que será a sua imagem.
Arcos côngruos
São arcos que possuem as extremidades num mesmo ponto. Para que isso ocorra, a diferença entre as suas medidas deve ser uma quantidade inteira de voltas, ou seja, ser múltiplo de 360° ou 2π radianos.
Ex.: acima, vimos que 30o e 390o são arcos côngruos.
Podemos deduzir uma expressão geral dos arcos côngruos:
AB = α + 2πK; α em radianos. (K ∈ Z)
AB = α + 360°.K; α em graus.
Linhas trigonométricas no ciclo
Á partir do ciclo trigonométrico, definem-se as principais linhas trigonométricas: seno, cosseno e tangente, da seguinte maneira:
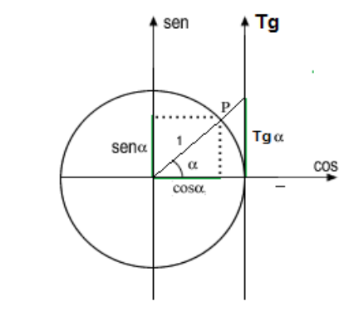
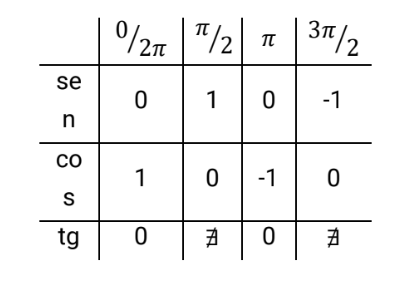
Percebemos que o sinal do seno, cosseno e tangente de um ângulo mudam de acordo com o quadrante em que o ângulo se encontra.

Observe que tanto o seno de a quando o cosseno de a pertencem ao intervalo [-1,1]