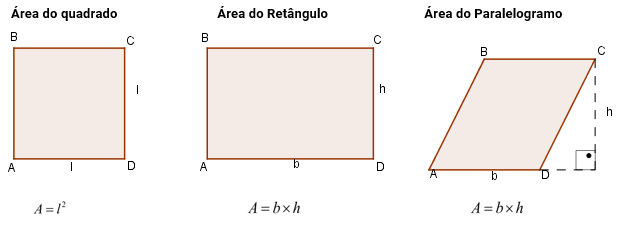
Área do retângulo, do quadrado e do paralelogramo
Área do triângulo
Área do losango e do trapézio
Área do círculo e suas partes
Área por partição e exclusão
Toda superfície plana ocupa uma extensão no plano. As áreas medem o tamanho da superfície dessas figuras planas já conhecidas. Na aula de hoje, vamos focar nas áreas das figuras que vimos anteriormente: quadriláteros e triângulos.
Triângulos
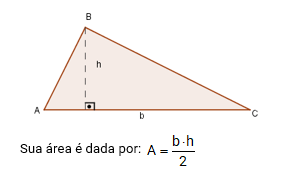
Considere um triângulo de base b e altura h:
Se o triângulo for equilátero (todos os lados iguais), temos que sua altura (h) vale:
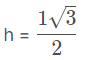
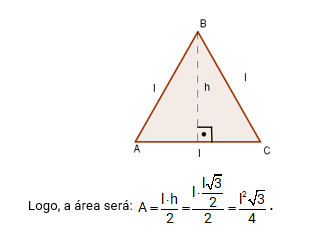
Considere o triângulo abaixo:
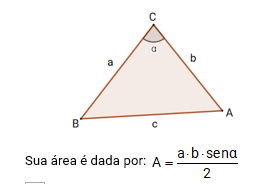
Por últimos, temos uma fórmula para cálculo de área de triângulos que é bem esquecida, mas é muito útil! É a fórmula de Heron!
Seja um triângulo de lados medindo a, b e c:
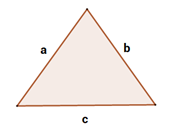
Sua área é dada pela fórmula de Heron:
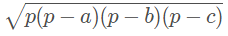
Em que p é o semiperímetro do triângulo, ou seja,
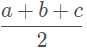
Quadriláteros
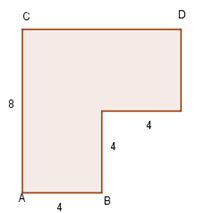
Podemos ter casos onde calcular a área apenas aplicando a fórmula não é possível como no exemplo abaixo:
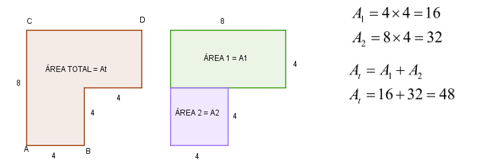
Apesar disso, podemos dividir esse polígono em outros polígonos que sabemos calcular as áreas:
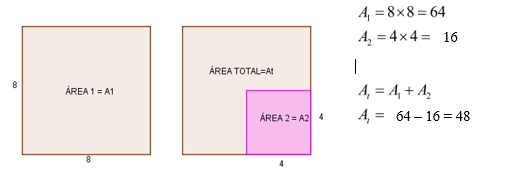
Um segundo modo de calcular essa área total seria:
Exemplo: Calcular a área da figura abaixo:
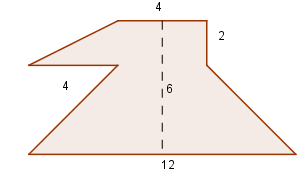
Resolvendo, nós temos as seguintes áreas:
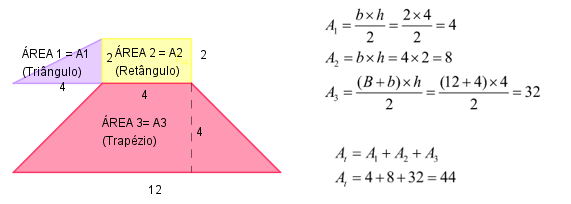
Circunferência
Circunferência é o lugar geométrico dos pontos no plano que estão à mesma distância em relação a um ponto central. Esta distância é chamada de raio.
Obs: Circunferência ≠ Círculo!
Círculo é toda a região do plano delimitado por uma circunferência.
Circunferência é apenas a linha que dá forma à figura.
Elementos de uma circunferência
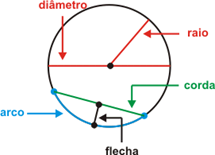
- Centro: ponto equidistante de todos os pontos da circunferência.
- Raio: distância entre o centro e qualquer ponto da circunferência.
- Arco: parte da circunferência delimitado por dois pontos.
- Corda: segmento de reta que une dois pontos da circunferência.
- Flecha: segmento de reta que liga o ponto médio da corda ao ponto médio do seu arco correspondente.
Comprimento da circunferência e de arcos

Dado uma circunferência com centro O e raio R, seu comprimento é dado pela seguinte fórmula:
C = 2πR
Área do círculo
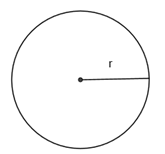
Dado um círculo de raio r, sua área é A = πr².
Área do setor circular
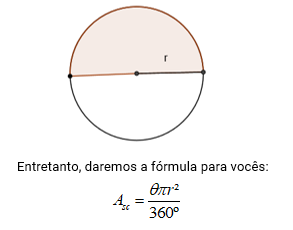
Para saber a área do setor basta lembrar que um setor é um pedaço do círculo e pode assim podemos usar regra de 3 para saber.
Por exemplo: Para saber a área de um setor circular de 180° e raio igual a 2 cm basta lembrar que o círculo completo tem 360° logo a área do setor será a metade da área do círculo. Nesse caso. A área do círculo será 4πr cm² e, portanto, a do setor será 2πr cm².
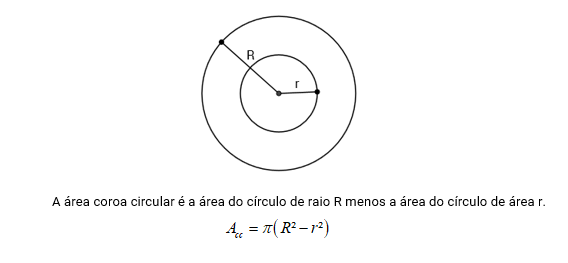
Área da coroa circular