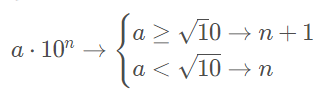Análise dimensional
Exemplos de análise dimensional
Notação científica
Exemplos de notação científica
Ordem de grandeza
Exemplos de ordem de grandeza
Algarismos significativos
Exemplos de algarismos significativos
Análise Dimensional
A análise dimensional é o estudo das grandezas físicas com relação às suas unidades de medida, portanto permeia todos os ramos da Física.
Grandezas Fundamentais
Grandezas físicas fundamentais formam um grupo limitado de grandezas que nos servirão de base para escrevermos outras grandezas que possam surgir adiante. As grandezas fundamentais são:
- Massa: M
- Comprimento: L
- Tempo: T
- Temperatura: θ
- Corrente Elétrica: I (Corrente elétrica é a quantidade de carga por unidade de tempo)
Unidade Dimensional
Cada grandeza física pode ser escrita como combinação de grandezas fundamentais. Em geral devemos ter uma expressão que define a grandeza estudada a partir de outras conhecidas. Veja como será a notação adotada para se referir a uma grandeza física A e a unidade dimensional de A.
A→ grandeza física
[A]→ unidade dimensional de A
Exemplo:
v→ velocidade
[v]→ ms (S.I.)
Em geral: [v]=LT=LT-1
Obs.: Por conveniência definimos a unidade dimensional de um número puro como sendo:
[n] = 1, se n é um número puro.
[cos α] = 1, cosseno de um ângulo real é um número puro.
Escrevendo um número em Notação Científica e Regras de Arredondamento
Para escrevermos um número em notação científica utilizamos o seguinte formato:
a x 10n
onde a∈R,1 ≤ a < 10, ou seja, a é um número real R maior ou igual a 1 e menor que 10, com apenas uma casa decimal, e n é um número inteiro qualquer.
No entanto, é fácil perceber que podemos ter problemas em escrever esses números, pois no caso de certos algarismos será necessária a realização de alguma aproximação para sua total adequação ao formato desejado da notação científica. Vejamos um exemplo:
150.000.000.000 = 1,5.1011 (a vírgula deslocou-se 11 casas para a esquerda).
Ordem de grandeza (OG)
Determinar a ordem de grandeza de uma medida consiste em fornecer, como resultado, a potência de 10 mais próxima do valor encontrado para a grandeza. Para isso é necessário comparar o valor de a com √10, tal que temos a seguinte regra: