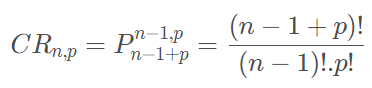Princípio fundamental da contagem (PFC)
Arranjo com repetição
Arranjo sem repetição
Fatorial e permutação
Anagrama
Anagrama com repetição
Análise Combinatória
Fatorial
O fatorial é uma operação aplicada apenas a número naturais e é definido da seguinte maneira: ∀m ∈ N temos:
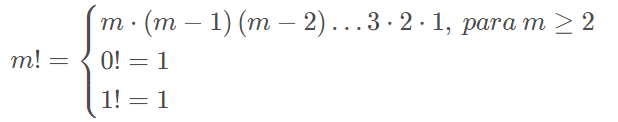
Princípio Fundamental da Contagem (PFC)
Essa técnica básica de contagem visa calcular o número de possibilidades de ocorrência de um evento E, composto por uma série de sub-eventos independentes: E1, E2, E3… Na composição do evento E, escolhe-se apenas umas das possibilidades de cada um de seus sub-eventos.
Representamos os totais de possibilidades pelas quais os eventos podem ocorrer por:
n(E): número de possibilidades do evento E
n(Ei): número de possibilidades do evento Ei
Podemos enunciar que o número de possibilidades de ocorrência do evento E é dado por:
n(E) = n(E)1.n(E)2…n(E)n
Permutações
Permutação simples de n objetos distintos
Dado um conjunto com n elementos distintos, chama-se permutação dos n elementos, todo arranjo desses n elementos tomados n a n
P = n!
Permutação com elementos repetidos
De modo geral, se temos n elementos dos quais n1 são iguais a a1, n2 são iguais a a2, n3 são iguais a a3 , … , nr são iguais a ar, o número de permutações possíveis é dado por:
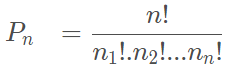
Arranjo
Dado um conjunto com n elementos distintos, chama-se arranjo dos n elementos, tomados p a p, a qualquer sequência ordenada de p elementos distintos escolhidos entre os n existentes.
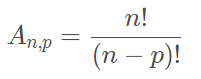
Combinação Simples
Número de combinações de n elementos tomados p a p onde a ordem não importa
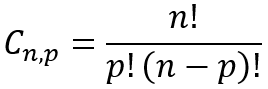
Permutação Circular
Permutação circular é um tipo de permutação composta por n elementos distintos em ordem cíclica (formando uma circunferência).
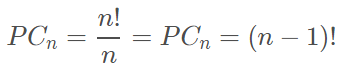
Combinações Completas
Combinações completas de n elementos, tomados p a p, são combinações de n elementos não necessariamente distintos. Em vista disso, quando vamos calcular as combinações completas devemos levar em consideração as combinações com elementos distintos (combinações simples) e as combinações com elementos repetidos.