Semelhança de polígonos em Matemática

Semelhança de Polígonos

Pegue uma figura e a aumente. Depois, a diminua. Temos 3 figuras com o mesmo desenho, só que de tamanhos diferentes. Dizemos, assim, que elas são semelhantes entre si.

Ex.: O logo do descomplica em tamanhos diferentes.

Agora, vamos formalizar esse conceito.

 Semelhança de polígonos

Polígonos são semelhantes quando possuem:

• Ângulos respectivamente iguais.
• Lados respectivamente proporcionais.

Vamos estudar o caso mais clássico de semelhança: Triângulos.

Semelhança de triângulos

Dois triângulos são semelhantes se possuírem os ângulos iguais. Na verdade, se garantirmos que 2 ângulos são iguais, já podemos dizer que são semelhantes, pois a soma dos ângulos internos de um triângulo é constante igual a 180 graus.

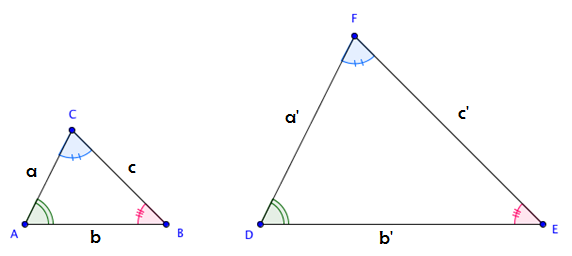
Temos que: 

 
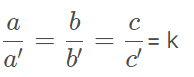
Dizemos que a e a’, b e b’, c e c’ são pares de lados homólogos e k é a razão de semelhança.
A razão de semelhança é válida para todas as medidas lineares (alturas, medianas e perímetro, por exemplo). E se quisermos calcular a razão entras as áreas de polígonos semelhantes? A razão entre as áreas será k2

Além disso, temos alguns casos em que a semelhança entre triângulos também ocorre:

• Caso LAL: dois triângulos que possuem dois lados congruentes e o ângulo formado por eles iguais são semelhantes.
• Caso LLL: dois triângulos que possuem todos os lados correspondentes proporcionais são semelhantes.

Consequência da semelhança de triângulos:

Seja ABC um triângulo onde D é ponto médio do lado AB e E é ponto médio do lado AC como mostra a figura abaixo

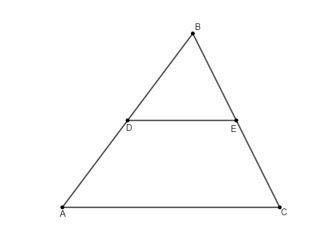
Temos que DE é o seguimento que liga os pontos médios. Podemos notar que os triângulos ABC e BDE são semelhantes já que BD = AB/2 e BE = AC/2 e ABC é ângulo comum a ambos triângulos. E, nesse caso, a razão de semelhança entre os lados ABC e BDE é de 2 para 1, em particular, DE= AC/2. Essa consequência é conhecida como base média de um triângulo.