Exercício 1 – Glicose
Exercício 2 - Sacarose
Exercício 3 - Metano
Exercício 4 - Água
Exercício 5 - O2 e SO3
Exercício 6 - Fórmula percentual
Exercício 7 – Cloreto de ferro III hidratado
Relações numéricas
Unidade de massa atômica
A unidade de massa atômica é uma unidade de medida de massa utilizada para expressar a massa de partículas atômicas. Ela é definida como 1/12 da massa de um átomo de carbono-12 em seu estado fundamental.

Massa atômica
A massa atômica de um elemento é a média da sua massa e ocorrência dos seus isótopos na natureza. A massa atômica do átomo é expressa em u ou uma.
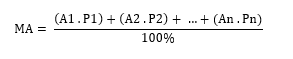
A = massa do isótopo
P = % de ocorrência do Isótopo
P1 + P2 + … + Pn = 100%
Ex.:
B10 ocorrência 20%
B11 ocorrência 80%
MA = (10 × 20 + 11 × 80) / 100%
MA = 10,8u
Número de massa
O número de massa de um elemento é dado pelo somatório da quantidade de prótons ou número atômico, com os de nêutrons existentes no núcleo.
A = p + n ou A = Z + n
Massa molecular
A massa molecular corresponde à soma das massas atômicas dos elementos que compõem uma determinada substância.
Massa molecular = ΣMA
Ex.: Dadas as massas atômicas: Ca = 40u, H = 1u, S = 32u, O = 16, C = 12u.
H2SO4 = 2 + 32 + 64 = 98u
CaCO3 = 40 + 12 + 48 = 100u
Número de avogadro
O número de Avogadro é a quantidade de entidades elementares (átomos, elétrons, íons, moléculas) presentes em 1 mol de qualquer substância.
1 mol = 6,02 x 10^23 unidades elementares
Ex.:
1 mol de H2SO4 possui 6.02 x 10^23 moléculas
1 mol de Fe possui 6.02 x 10^23 átomos
Massa molar
É a massa em gramas presente em 6,02 x 10^23 unidades elementares de determinada espécie, ou seja, a massa presente em 1 mol de qualquer substância. Numericamente as massas atômica e molar são iguais.
Ex.:
1 mol O2 = 6,02 x 10^23 moléculas de O2 = 32g de massa molar
1 mol H2SO4 = 6,02 x 10^23 moléculas de H2SO4 = 98g de massa molar
1 mol Fe = 6,02 x 10^23 átomos de Fe = 56g de massa molar
Volume molar
O volume molar é o volume ocupado por 1 mol de qualquer gás, esse volumo pode se alterar com a variação da pressão e da temperatura, em módulos posteriores aprofundaremos o cálculo do volume de gases onde há essa variação na pressão e na temperatura.
Volume molar nas CNTP
1 mol = 22,4 litros
CNTP = Condições normais de temperatura e pressão, Em que a pressão é igual a 1 atm e a temperatura é de 273 K (0ºC).
Para provarmos que 1 mol de qualquer gás nas CNTP ocupa o volume de 22,4L, podemos jogar tais valores na equação de Clapeyron.
P . V = n . R . T
Onde:
P = pressão (atm)
V = volume (litros)
n = número de mol
R = constante dos gases (valor = 0,082 L.atm / mol.k)
T = temperatura (Kelvin)
Para gases nas CNTP:
P . V = n . R . T
1 . V = 1 . 0,082 . 273
V = 22,4L
Importante!
CATP = Condições Ambientais de Temperatura e Pressão, em que a pressão também é de 1 atm, mas a temperatura é de 298 K (25 ºC), o volume molar passa a ser 25 L, ou seja, 1 mol = 25 litros.
P . V = n . R . T
1 . V = 1 . 0,082 . 298
V = 25L
Ex.:
Nas CNTP:
1 mol O2 = 22,4L
2 mol O2 = 44,8L
½ mol N2 = 11,2L
Volume molar fora das CNTP
Para calcular os volumes molares fora das CNTP, utilizamos a equação de Clapeyron.
P . V = n . R . T
Onde:
P = pressão (atm)
V = volume (litros)
n = número de mol
R = constante dos gases (valor = 0,082 L . atm/mol. K)
T = temperatura (Kelvin)
Ex.:
Qual o volume ocupado por 1 mol de O2 a 2 atm e 100k.
P . V = n . R . T
2 . V = 1 . 0,082 . 100
V = 16,4L de O2