Exercícios de Cinética Química em Química

Cinética é um termo que denota movimento. Na física, a ciência assim denominada estuda o movimento dos corpos. A cinética química, então, estuda o movimento das reações químicas, ou seja, as velocidades com que elas ocorrem, e ela possui diversas aplicações práticas importantes para o nosso dia a dia: como desacelerar o apodrecimento dos alimentos, como acelerar cozimentos, como produzir com rapidez alguma substância que, de forma natural, levaria muito tempo, etc.

Velocidades das reações

Existem reações que duram segundos e outras que levam anos para se concluírem. Mas como se mede a velocidade com que uma reação ocorre?
Uma reação química, como sabemos, possui reagente(s), que é(são) consumido(s), e produto(s), que é(são) formado(s) ao longo do decorrer da reação. Ou seja, uma reação, num primeiro momento, possui apenas reagente(s), cuja quantidade diminui ao longo do seu decorrer. Após um tempo é que o(s) produto(s) – quantidade inicial igual a zero – começa(m) a aparecer e a ter sua quantidade aumentada ao longo do decorrer da reação.
Se anotamos a hora de início de determinada reação química e, após muito tempo, a quantidade de reagentes for só um pouco menor que a quantidade inicial e a quantidade de produtos for só um pouco maior que a quantidade inicial (zero), entendemos que a reação está ocorrendo de forma lenta. Por outro lado, caso a variação das quantidades de reagentes e produtos tenha sido grande, entendemos que a reação está **rápida. **
Diante disso, fica claro que o cálculo da velocidade de uma reação consiste no cálculo da velocidade de consumo do(s) reagente(s) ou da velocidade de formação do(s) produto(s).

Velocidade média

A velocidade com que uma reação ocorre não é constante, havendo momentos de maior rapidez e outros de maior lentidão. Por isso, calculamos a velocidade média, que consiste na **divisão do quanto uma substância variou **por quanto tempo se passou, desde o início da reação até o momento em que a quantidade da tal substância foi contada.

Importante:
• A quantidade do reagente ou do produto, na equação, pode ser expressa em mol, mol/L, g, g/L e em unidades de volume no caso dos gases (L, m³, etc).
• O tempo decorrido pode ser expresso em h, min ou s.
• Como a quantidade de reagente diminui ao longo do tempo, a quantidade final será menor que a inicial, o que nos dará uma variação de valor negativo. Veja um exemplo:

• Quantidade inicial = 8 mol/L
• Quantidade final = 2 mol/L

Δ quantidade = 2 mol/L – 8 mol/L = – 6 mol/L

Neste caso, devemos ignorar esse sinal e dizer que a taxa de consumo de reagente foi de 6 mol/L. Matematicamente, isso significa dizer que o cálculo da taxa de consumo de um reagente deve ser expressado em módulo

Tx(consumo do reagente) = |quantidade final – quantidade inicial|

ou então com o sinal de menos na frente
Tx(consumo do reagente) = – (quantidade final – quantidade inicial)

A taxa de formação de um produto, no entanto, não é calculada dessa forma, visto que a quantidade ou concentração final sempre é maior que a inicial. Usa-se, normalmente,

Tx(formação do produto) = (quantidade final – quantidade inicial)

Exemplo: Na reação C6​​H1​​2​​O​6​​ + 6O2​​ → 6 CO​2​​ + 6 H​2​​O, calculam-se as concentrações (em mol/L) de glicose em alguns intervalos de tempo.

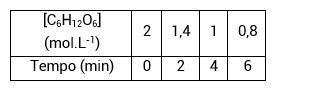
Vamos calcular a velocidade média dos seguintes intervalos:

Como nós conhecemos as proporções estequiométricas da reação (1 C6​​H1​​​2​​O​6​​ : 6 O​2​​ : 6 CO​2​​ : 6 H2​​O), podemos descobrir a velocidade de consumo do O2​​ e de produção de CO​2​​ e H2​​O.
Observe que a proporção da glicose em relação aos demais é igual:

1 mol/L C​6​​H1​​​2​​O​6​​ ----- 6 mol/L O​2​​ ----- 6 mol/L CO2​​ ----- 6 mol/L H2​​O

Com isso, vamos calcular:
• No intervalo de 0 a 6 min, a velocidade de consumo de O2​​:

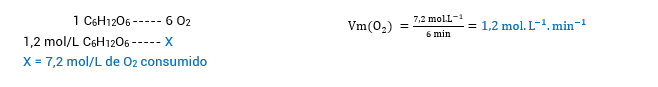
Obs: Como a proporção do consumo de C​6​​H​1​​​2​​O_6​​ em relação à produção de CO2 e H​2​​O é a mesma do consumo de O​2​​, a quantidade de CO2 e H2O produzidos será igual à quantidade de O​2​​ consumido. Por isso, vamos continuar calculando, para os demais intervalos, a velocidade de O2​​, CO2​​ e H​2​​O ao mesmo tempo.

Agora, vamos comparar as velocidades de O2, CO2 e H2O com as de C6H12O6:

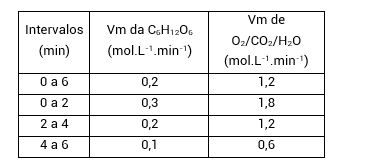
Analisando essa tabela, percebemos que as velocidades médias de O2, CO2 e H2O também obedecem à proporção 6:1 em relação às velocidades de C6H12O6, já que são 6 vezes maiores que as velocidades de consumo de C6H12O6.
Concluímos, assim, que o valor de Vm de cada composto da reação dividido pelo seu coeficiente estequiométrico sempre vai ser igual ao valor de Vm dos demais compostos da reação divididos pelos seus coeficientes estequiométricos, como podemos ver abaixo:

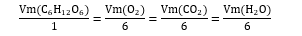
Este valor comum é considerado o valor da velocidade média da reação. Logo, generalizamos da seguinte forma:

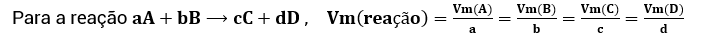
Lei da velocidade

Conhecimentos prévios importantes:
Reações elementares são aquelas que ocorrem em apenas uma etapa. Exemplo:

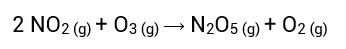
Reações não elementares são aquelas que ocorrem em duas ou mais etapas, sendo uma lenta e as demais rápidas.

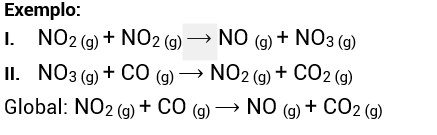
Sabe-se que a concentração dos reagentes de uma reação química influi na velocidade com que ela vai ocorrer. Aumentando a concentração de um e/ou de outro reagente, a velocidade da reação também aumenta. Diminuindo a concentração, a velocidade também diminui.

Dois cientistas (Guldberg e Waage), ao estudarem as variações nas velocidades das reações com o acréscimo ou a retirada de reagentes, perceberam que cada reação tem sua velocidade alterada seguindo um padrão, que depende apenas da temperatura do meio. Esse padrão definiu que cada reação possui sua constante de velocidade (k).
Notaram, ainda, que, para as reações elementares, a velocidade aumenta igual ao aumento da concentração do reagente elevado ao coeficiente desse mesmo reagente. Ou seja, se a reação é 2A + B ⟶ C e eu multiplico a concentração de A por 2, a velocidade ficará multiplicada por 2² (4). Já se eu multiplico a concentração de B por 2, a velocidade ficará multiplicada por 2¹ (2).

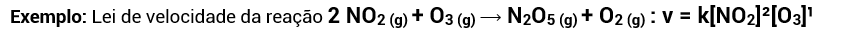
Para as reações não elementares, no entanto, a velocidade aumenta igual ao aumento da concentração dos reagentes da etapa lenta da reação elevados aos seus coeficientes estequiométricos.

Obs:
• Não é necessário representar expoentes 1, pois estes ficam implícitos;
• A questão tem que dizer qual é a etapa lenta ou te dar meios para descobrir isso (geralmente acontece quando a lei de velocidade é dada na questão).

Importante:

• Estes expoentes são chamados de ordem da reação. No caso acima, a ordem da reação para NO2 é 2 (2ª ordem). A soma das ordens de reação de cada reagente nos dá a ordem total da reação. No caso acima, a ordem total da reação é 2 (2ª ordem), visto que só há um reagente com expoente 2. Caso houvesse mais um reagente na lei de velocidade, com ordem 1, por exemplo, a ordem total da reação seria 3 (3ª ordem);
• À série de etapas de uma reação química, chamamos mecanismo de reação.

Como há essa diferença entre os expoentes das concentrações dos reagentes de reações elementares e de não elementares, Guldberg e Waage definiram que tais expoentes devem ser determinados experimentalmente, isto é, faz-se experimentos com valores diferentes das concentrações de cada reagente e mede-se as velocidades obtidas.

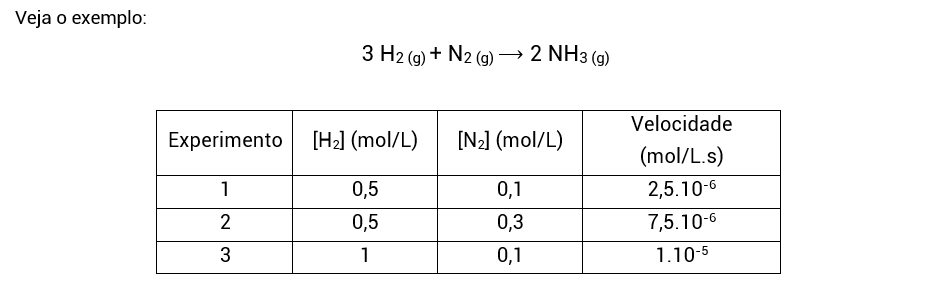
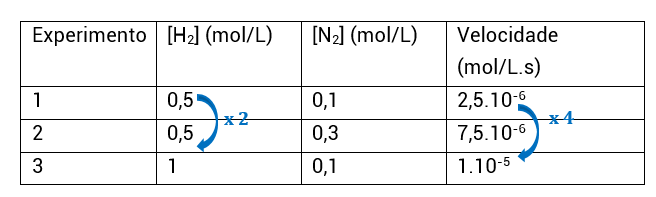
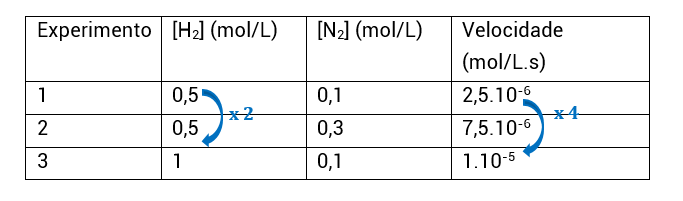
Do experimento 1 para o experimento 2, a concentração de H2 não foi alterada, enquanto a de N2 foi. Com isso, sabemos que a análise desses experimentos nos permitirá encontrar o expoente do N2, isto é, a ordem de reação em relação ao N2.
Ocorre assim:
• No modo mais detalhado, a gente faz uma relação entre as velocidades do experimento 1 e do experimento 2. Quando você vir relação entre equações, leia divisão. Além da divisão, podemos igualar o k1 com k2, uma vez que a constante de velocidade (k) é sempre igual para duas reações iguais em temperaturas iguais (mesmo que os componentes dessas reações estejam em concentrações molares diferentes). Aqui eu vou utilizar a divisão das leis de velocidade

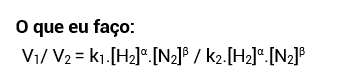
Do experimento 1 para o experimento 3, a concentração de N2 não foi alterada, enquanto a de H2 foi. Com isso, sabemos que a análise desses experimentos nos permitirá encontrar o expoente do H2, isto é, a ordem de reação em relação ao H2.

• O procedimento é idêntico ao anterior, só que pegamos as informações dos experimentos 1 e 3:

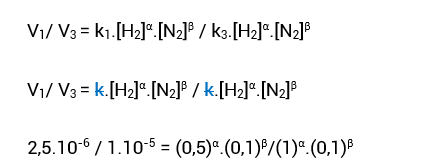
• Repare que V3​​ = 10​​^-5​​​. Colocando em base 10^−​​​6​​, fica V​3​​ = 10.10^−​​​6​​

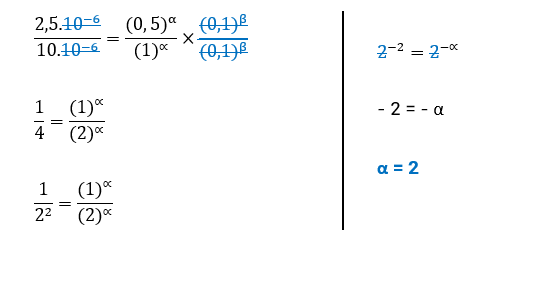
• Concluímos, assim, que a ordem de reação para H2 é 2.
Este procedimento, contudo, é muito longo e formal. Na prática, iremos utilizar um muito mais simples, que, com o treino, permitirá você saber a ordem de reação (α e β) apenas olhando para a tabela e fazendo poucos cálculos mentais. É o seguinte:

• Assim como o procedimento anterior, a gente seleciona dois experimentos em que a concentração de um dos reagentes permaneça constante e a do outro varie;

• Experimentos 1 e 2: H2 constante e N2 varia; ou seja, encontraremos β;

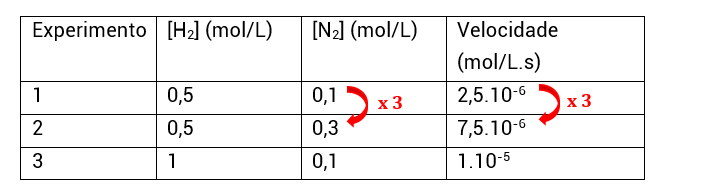
• Como vemos, a concentração de N2 é multiplicada por 3 e a velocidade também. O quanto [N2] variou elevado a β tem que ser igual ao quanto a velocidade variou:
3β = 3
3β = 3¹
β = 1

• Experimentos 1 e 3: N2 constante e H2 varia; ou seja, encontraremos α;

• Como vemos, a concentração de H2 é multiplicada por 2 e a velocidade é multiplicada por 4, ou seja, 2². O quanto [H2] variou elevado a α tem que ser igual ao quanto a velocidade variou:
2α = 4
2α = 2²
α = 2

• Agora, ao fim desse processo, podemos determinar que a lei de velocidade é v = k.[H2]².[N2] e que a ordem da reação é 3 (α + β = 2 + 1 = 3), ou seja, esta é uma reação de 3ª ordem.

Diante de tudo isso, Guldberg e Waage cunharam a lei da velocidade, lei de Guldberg-Waage, lei de ação das massas ou lei cinética, que diz o seguinte: a velocidade de uma reação química é diretamente proporcional ao produto das concentrações molares dos reagentes elevados a expoentes determinados experimentalmente.

Molecularidade

A molecularidade de uma reação elementar nos indica a quantidade de moléculas que reagiram para formar os produtos da reação. Se na reação ocorre somente o rearranjo ou a decomposição de 1 molécula reagente, ela é unimolecular. Se ocorre choque entre 2 moléculas reagentes, ela é bimolecular. Se ocorre choque entre 3 moléculas reagentes, é trimolecular

Repare que a molecularidade, nas reações elementares, pode ser encontrada pela soma dos coeficientes estequiométricos dos reagentes ou determinada pela ordem de reação (v = [NO​2​​]²[O​3​​], 3ª ordem).

Nas reações não elementares, determinaremos a molecularidade de cada etapa do mecanismo de reação separadamente, visto que cada etapa da reação consiste em uma reação elementar.

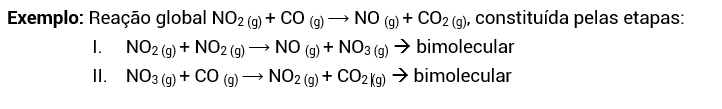
Concluímos, assim, que a ordem de reação para H2 é 2.
Este procedimento, contudo, é muito longo e formal. Na prática, iremos utilizar um muito mais simples, que, com o treino, permitirá você saber a ordem de reação (α e β) apenas olhando para a tabela e fazendo poucos cálculos mentais. É o seguinte:

• Assim como o procedimento anterior, a gente seleciona dois experimentos em que a concentração de um dos reagentes permaneça constante e a do outro varie;

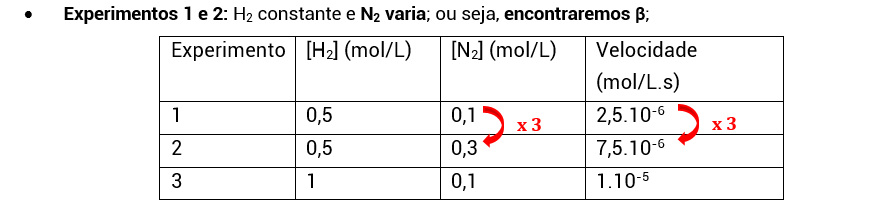
• Como vemos, a concentração de N_2​2​​ é multiplicada por 3 e a velocidade também. O quanto [N_2​2​​] variou elevado a β tem que ser igual ao quanto a velocidade variou:
3β = 3
3β = 3¹
β = 1

• Experimentos 1 e 3: N​2​​ constante e H2​​ varia; ou seja, encontraremos α;

Como vemos, a concentração de H2 é multiplicada por 2 e a velocidade é multiplicada por 4, ou seja, 2². O quanto [H2] variou elevado a α tem que ser igual ao quanto a velocidade variou:
2α = 4
2α = 2²
α = 2
• Agora, ao fim desse processo, podemos determinar que a lei de velocidade é v = k.[H2]².[N2] e que a ordem da reação é 3 (α + β = 2 + 1 = 3), ou seja, esta é uma reação de 3ª ordem.

Diante de tudo isso, Guldberg e Waage cunharam alei da velocidade, lei de Guldberg-Waage, lei de ação das massas ou lei cinética, que diz o seguinte: a velocidade de uma reação química é diretamente proporcional ao produto das concentrações molares dos reagentes elevados a expoentes determinados experimentalmente.