Exercícios sobre estequiometria em Química

Grau de pureza

Quando os reagentes não são substâncias puras (Grau de pureza) Em alguns casos na estequiometria os reagentes da reação apresentam em sua composição impurezas, principalmente em reações industriais, ou porque são mais baratos ou porque já são encontrados na natureza acompanhados de impurezas (o que ocorre, por exemplo, com os minérios). Consideremos o caso do calcário, que é um mineral formado principalmente por CaCO3 (substância principal), porém acompanhado de várias outras substâncias (impurezas). Digamos que tenhamos 100kg do mineral calcário, porém, 90kg são compostos por CaCO3 , que é o componente principal desse minério e o que necessariamente vai reagir numa reação química qualquer. Sendo assim, dizemos que 90% de todo minério recolhido é CaCO3 , logo, 10kg são apenas impurezas, que, geralmente, não reagem e não entram no cálculo estequiométrico. Com essa análise chegamos a conclusão que essa amostra de minério tem 90% de pureza, ou seja, dos 100kg que nós recolhemos 90kg serão utilizados.

Sendo assim, define-se: Porcentagem ou grau de pureza é a porcentagem da massa da substância pura em relação à massa total da amostra.

Vejamos um exemplo:
Uma amostra de calcita, contendo 80% de carbonato de cálcio, sofre decomposição quando submetida a
aquecimento, segundo a equação abaixo:

CaCO​3​​ → CaO + CO​2​​

Qual a massa de óxido de cálcio obtida a partir da queima de 800 g de calcita?

Resolução:
O enunciado nos diz que a calcita contém apenas 80% de CaCO3 . Temos então o seguinte cálculo de
porcentagem:

1ª linha) 800 g de calcita _________ 100%
2ª linha) x g de CaCO3 _________ 80% de - Grau de pureza
X = 640g de CaCO3​​ puro

Note que é apenas essa massa (640g de CaCO3​​ puro) que irá participar da reação. Assim, teremos o seguinte cálculo estequiométrico:

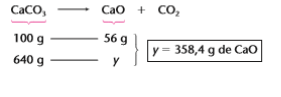
Exemplo 2:
Deseja-se obter 180 L de dióxido de carbono, medidos nas condições normais de temperatura e pressão, pela calcinação de um calcário com 90% de pureza de CaCO_3​3​​ (massas atômicas: C = 12; O = 16; Ca = 40).
Qual é a massa de calcário necessária?

CaCO​3​​ → CaO → CO2​​

Resolução:

Esta questão é do “tipo inverso” da anterior. Na anterior era dada a quantidade do reagente impuro e pedida a quantidade do produto obtido, agora é dada a quantidade do produto que se deseja obter e pedida a quantidade do reagente impuro que será necessária. Pelo cálculo estequiométrico normal, teremos sempre quantidades de substâncias puras:

A seguir, um cálculo de porcentagem nos dará a assa de calcário impuro que foi pedida no problema:

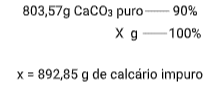
Note que a massa obtida (892,85g) é forçosamente maior que a massa de CaCO​3​​ puro (803,57g) obtida no cálculo estequiométrico, pois na massa do minério encontrada está contida as impurezas.

Rendimento

Vamos considerar a reação:
C + O​2​​ → CO​2​​

Supondo que deveriam ser produzidos 100 litros de CO2 (CNTP);
vamos admitir também que, devido a perdas, foram produzidos apenas 90 litros de CO2(CNTP), logo o
rendimento foi de 90%.

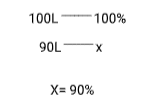
Em casos assim, dizemos que:

Rendimento é o quociente entre a quantidade de produto realmente obtida em uma reação e a quantidade que teoricamente seria obtida, de acordo com a equação química correspondente.

Exemplo:

Num processo de obtenção de ferro a partir da hematita (Fe​2​​O3​​), considere a equação balanceada:

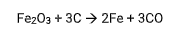
Massas atômicas: C = 12; O = 16; Fe = 56

Utilizando-se 4,8 toneladas (t) de minério e admitindo-se um rendimento de 80% na reação, a quantidade de ferro produzida será de:

a) 2.688 kg
b) 3.360 kg
c) 1.344 t
d) 2.688 t
e) 3.360 t

Resolução: Após o balanceamento da equação, efetuamos o cálculo estequiométrico da forma usual

Gases fora das CNTP

Definimos a equação geral dos gases de Clapeyron para usar em gases que não estejam nas CNTP, ela é dada por:
PV = nRT

Podemos expressar o número de mol (n) da seguinte maneira também:
PV = m/MM RT

Onde:
P = Pressão do gás (atm)
V = Volume do gás (L)
n = Quantidade do gás (mol)
m = Massa do gás (g)
M.M = Massa molar do gás(g)
R = Constante universal dos gases perfeitos (L.atm/mol.k​​)
T = Temperatura do gás (medida em Kelvin)

Volume molar fora das CNTP (Condições Normais de Temperatura e Pressão)

Definimos que uma substância está fora das CNTP se as condições de temperatura e pressão são diferentes de 0ºC e 1 atm. Quando são usados valores diferentes para esses parâmetros calculamos seu
volume a partir da equação de Clapeyron.

Exemplo:

Dada a reação: Fe​2​​O​3​​(s) + 3CO(g) --> 2Fe(s) + 3CO​2​​(g)

Sabendo que a massa de um mol de ferro é de 56g, calcule a massa de ferro produzida quando 8,2L de CO2​​ são formados a 2 atm e 127ºC.

Resolução:
Primeiramente amos calcular quantos litros de CO​2​​ são produzidos quando, nas mesmas condições de temperatura e pressão dadas no texto, temos 3 mol do mesmo(quantidade estequiométrica de mol de gás CO​2​​)

PV =nRT
2.V = 3 . 0,082 . 400
V = 49,2L

Assim, quando se produz 2 mol de ferro nas condições dadas eu produzo 49,2L de CO​2​​, com uma regra de três, consigo estabelecer quantas gramas de ferro eu produziria com 8,2L de CO​2​​.

2x56 gramas de ferro ______ 49,2L de CO​2​​
Y gramas de ferro ______ 8,2L de CO​2​​

Y = 18,7g de ferro (aproximadamente)

Reação com reagente em excesso ou limitante

Toda reação química ocorre de acordo com a proporção estequiométrica constante, indicada pelos seus coeficientes. Porém, em alguns casos, teremos um dos reagentes sendo totalmente consumidos e outro com excesso(sobra) no final da reação. O reagente totalmente consumido neste tipo de reação é chamado reagente limitante. E o reagente com “sobra” será chamado reagente em excesso.

Exemplo 1:
3H​2​​ + N2​​ ↔ 2NH​3​​

Possui proporção estequiométrica de:
3 mols H2​​ + 1 mol de N​2​​  ⇌ 2 mols de NH​3​​
Proporção: 3 : 1 : 2

Se quiser produzir o triplo de NH​3​​ , precisamos manter a proporção:
9 mols H2​​ + 3 mols de N​2​​  ⇌ 6 mols de NH​3​​
Proporção: 9 : 3 : 6

No entanto, se estiver reagindo:
6 mols H​2​​ + 4 mols de N​2​​  ⇌ 4 mols de NH​3​​
Proporção dada: 6 : 4 : 4 - A reação possui mais N2​​ do que o necessário.
Proporção correta: 6 : 2 : 4
O N​2​​ está em excesso: 2 mols de excesso
O H2​​ é o reagente limitante, pois é totalmente consumido.

Exemplo 2:
Qual o reagente em excesso e qual o reagente limitante quando reagimos 128g de SO2​​ com 48g de O2​​ .

Massa molar: S = 32g/mol, O = 16g/mol.

SO2 + 1/2 O2​​ ⇌ SO​3​​

Possui proporção estequiométrica de:
1 mol SO 2 + ½ mol de O2​​  ⇌ 1 mol de SO3​​
Proporção em mol: 1 : ½ : 1
Proporção em massa: 64g : 16g : 80g

Se quiser reagir 128g de SO_2​2​​ com 48g de O2​​ , precisamos manter a proporção:

64g de SO​2​​ reage com 16g de O​2​​  
128g (2 x 64) de SO2​​ reagiria também com o dobro de O2​​ , 32g.

Como se pode observar os 128g de SO2 reagem, portanto ele é o reagente limitante. E somente 32g de O​2​​ precisam reagir para consumir toda a massa de SO2​​ e como temos 48g de O​2​​ , 16g do mesmo estão em excesso, ou seja, 16g de O​2​​ não reagem (sobram).

Reações consecutivas

Para que seja possível relacionar substâncias que dão sequência a reações consecutivas, é preciso que haja
uma substância comum entre elas. Sendo assim, será possível determinar coeficientes comum entre essas
equações.

São reações consecutivas, por exemplo:

S​8​​ + O​2​​ → SO​2​​
SO2​​ + ½ O​2​​ →  SO​3​​
SO4 + H2O → H2SO4

Nota-se que o SO​2​​ é comum a equação 1 e 2, e o SO​3​​ é comum a equação 2 e 3. Sendo possível criar uma relação entre as três equações.

Sendo assim, para cada 8 mols de S8​​ pode-se produzir quantos mols de H​2​​SO​4​​?

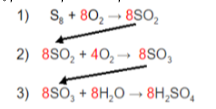
Pode-se produzir 8 mols de H_2​2​​SO_4​4​​ a partir de 1 mol de S_8​8​​

Exemplo:
Qual a massa de CO2​​ produzida pela queima de 36g de C com excesso de O​2​​

C + ½ O2​​ → CO
CO + ½ O​2​​ → CO​2​​

Pela estequiometria da reação sabemos que:
12g de C produz 28g de CO, e 28g de CO produz 44g de CO​2​​.

Logo,
36g (3 x 12g) de C produz 84g (3 x 28g) de CO, e 84g de CO produz 144g (3 x 44g) de CO​2​​ . Mantendo assim a proporção existente entre as equações intermediadas pelo CO.