Definição
Aprenda sobre equação de segundo grau. Confira!
Equação incompleta: b = 0
Equação incompleta: c = 0
Equação completa: fórmula de Báskara
Discussão das raízes
Relações entre coeficientes e raízes
Definição
É toda equação que pode ser reduzida à forma:
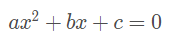
Com a,b,c ∈ R e a ≠ 0. a,b,c são chamados de coeficientes.
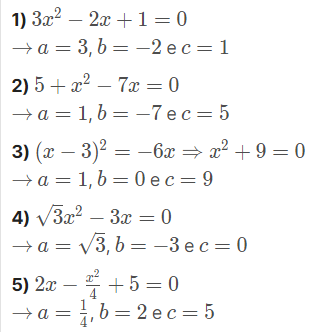
Obs: Os exemplos 1, 2 e 5 são chamados de equações completas pois possuem todos os coeficientes, já os os exemplos 3 e 4 são chamados de equações incompletas pois não possuem todos os coeficientes.
Equação incompleta: b = 0
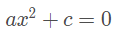
Exemplos:
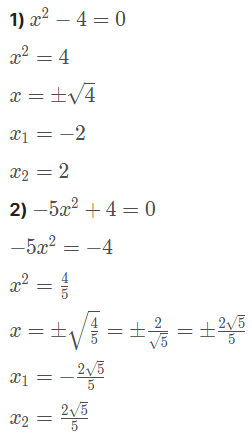
Equação incompleta: c = 0
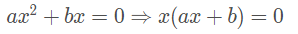
Exemplos:
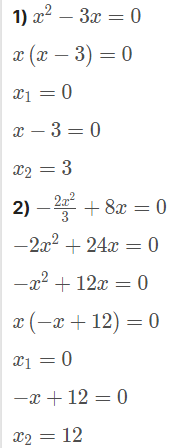
Equação completa: fórmula de Bhaskara
Quando a equação do segundo grau é completa, para encontrar as raízes, deve-se usar a fórmula de Bhaskara.
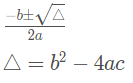
Obs: Delta (△) é chamado de discriminante.
Exemplos:
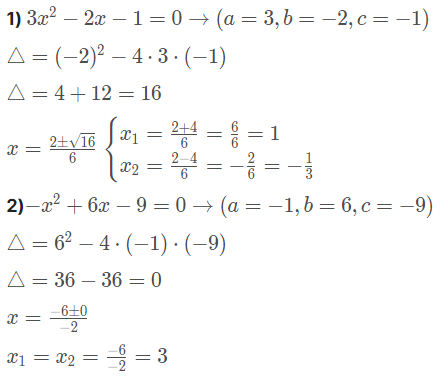
Discussão das Raízes

Relações entre coeficientes e raízes
É possível encontrar as raízes de uma equação do segundo grau através de relações entre os coeficientes. Chamamos este método de “soma e produto”. Observe:
Soma das raízes
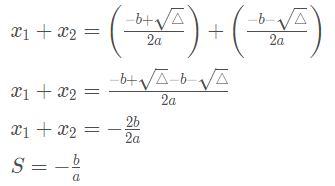
Produto das raízes
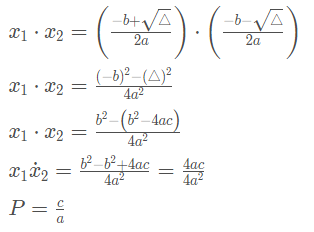
Portanto as raízes de uma equação serão os dois números que somados resultarão em -b/a e multiplicados resultarão em c/a.